白话机器学习算法 Part 2
2019年04月07日 由 sunlei 发表
221853
0

本文是《白话机器学习算法》系列文章第二部分,第一部分(白话机器学习算法 Part 1)中我们介绍了:
- 梯度下降法/最佳拟合线
- 线性回归(包括正则化)
- 领回归&套索回归
今天,我们继续了解其他的机器学习算法。
01.逻辑回归Logistic Regression
线性回归=线性回归=一些变量对另一个变量的影响,假设1)结果变量是连续的,2)变量与结果变量之间的关系是线性的。
但是如果你的结果变量是“绝对的”呢?这就是逻辑回归的作用!
分类变量就是只能属于单一类别的变量。举一个很好的例子:一周有几天——如果你有一堆关于星期几发生的事情的数据点,那么你就不可能得到一个可能发生在星期一到星期二之间的数据点。如果周一发生了什么事,那就是周一发生的,故事到此结束。
但是,如果我们考虑线性回归模型的工作原理,我们如何能够找出最适合某个类别的一条线呢?那是不可能的!这就是为什么逻辑回归模型输出数据点在一个或另一个类别中的概率,而不是一个常规数值。这就是为什么逻辑回归模型主要用于分类的原因。
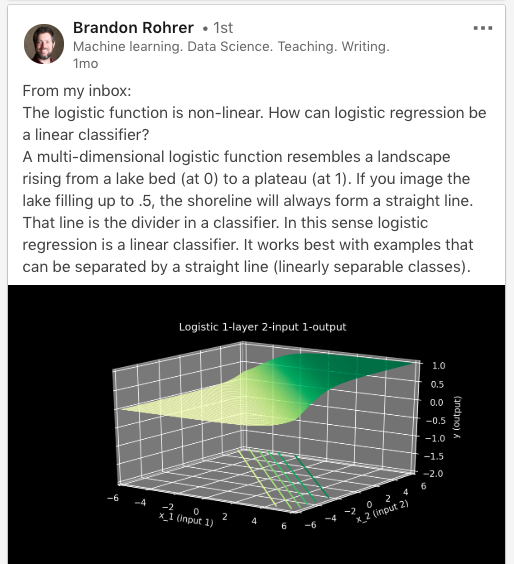
但是回到线性回归和逻辑回归都是“线性的”。“如果我们找不到一条最适合逻辑回归的直线,那么逻辑回归的线性部分又在哪里呢?”在逻辑回归的 世界里,结果变量与自变量的对数几率比呈线性关系。
但是对数几率究竟是多少呢?好了,我们开始…
02.几率Odds
逻辑回归的核心=几率。
直观地说,几率是我们能够理解的——它们是成功的概率到失败的几率。换句话说,它们是发生某件事的几率与不发生某件事的几率比。
举一个具体例子,我们可以想到一个班级的学生。假设女性通过测试的几率是5:1,而男性通过测试的几率是3:10。这意味着,在6名女性中,有5名可能通过测试,而在13名男性中,有3名可能通过测试。这里总共有19名学生(6名女生+ 13名男生)。
那么……几率和概率是不一样吗?
遗憾的是,不!几率是指某件事情发生的次数与所有事情发生的总次数之比(如10次正面出局30次投币),概率是指某件事情发生的次数与未发生的次数之比(如10次正面出局20次反面出局)。
这意味着,虽然概率总是限制在0-1的范围内,但几率可以不断地从0增加到正无穷大!这给我们的逻辑回归模型带来了一个问题,因为我们知道我们的预期输出是一个概率(即0-1之间的一个数字)。
那么,我们如何从几率到概率呢?
让我们考虑一个分类问题…比如说你最喜欢的足球队赢了另一个足球队。你可能会说你的球队输的几率是1:6,或者0.17。你的球队获胜的几率是6:1或6,您可以在下面的数字行中表示这些赔率:
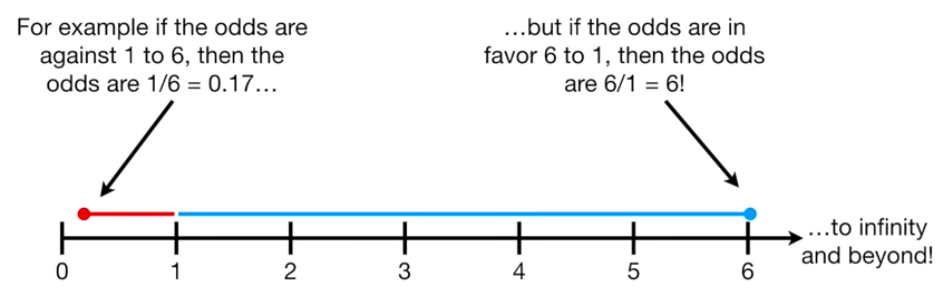
现在,你不希望你的模型预测你的球队会在未来的比赛中获胜,仅仅是因为他们过去获胜的几率比他们过去失败的几率大得多,对吧?还有很多你想让你的模型考虑的因素(可能是天气,可能是首发球员等等)!所以,为了得到均匀分布或对称的几率大小,我们计算了对数几率。
03.对数几率Log-Odds
对数几率是指取几率的自然对数的一种简略方法。当你取某个数的自然对数时,它更趋于正态分布。当我们让一些东西做为正态分布时,我们本质上是把它放在一个非常容易使用的情况之下。
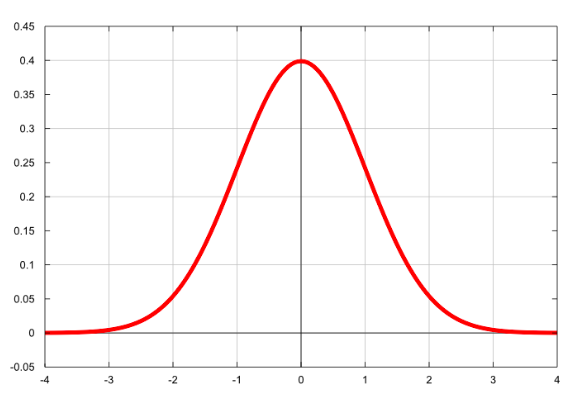
当我们计算几率时,我们将几率的范围从0-正无穷变换为负无穷-正无穷。你可以在上面的钟形曲线图上看到。
即使我们仍然需要输出的在0-1之间,我们通过取对数几率实现的对称性使我们比以前更接近我们想要的输出结果!
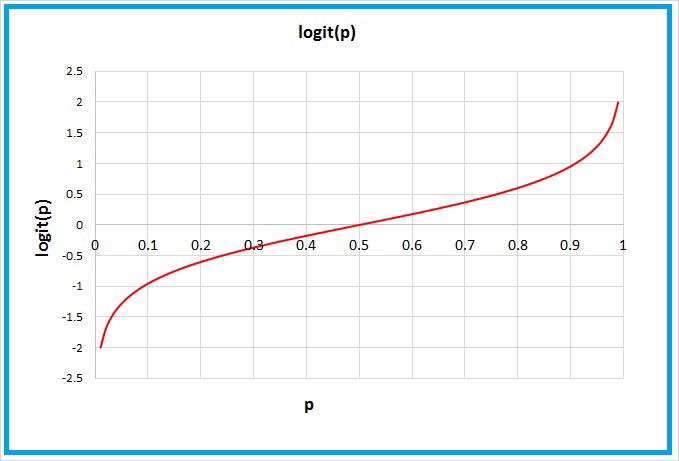
04.逻辑函数Logit Function
逻辑函数只是我们计算对数几率的数学方法!
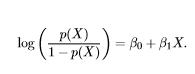
逻辑函数通过取自然对数,将几率选在负无穷到正无穷的范围内。
05.Sigmoid 函数Sigmoid Function
OK,但是我们还没有到我们的模型给出概率的之前,现在我们只知道从负无穷大到正无穷大的范围内的数字。输入:Sigmoid 函数。
以s形命名的sigmoid函数,恰好是log-odds的倒数。通过取log-odds的倒数,我们将我们的值从负无穷-正无穷映射到0-1。这反过来,让我们得到概率,这正是我们想要的!
相对于logit函数的图像y值从负无穷到正无穷,sigmoid函数的图像y值从0到1。
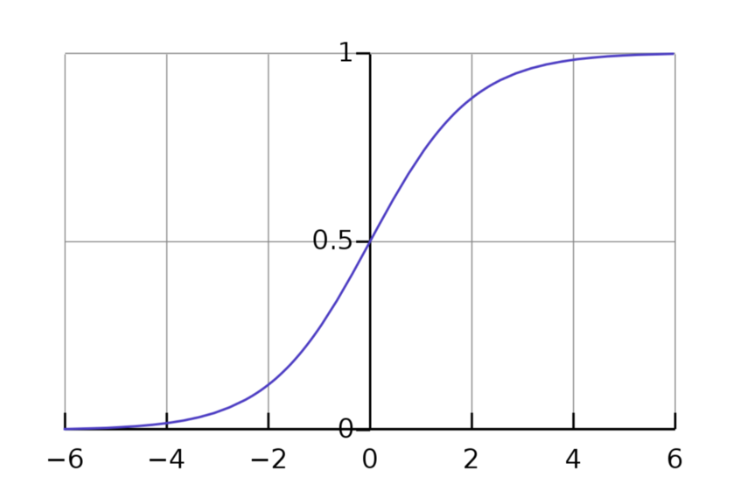
有了这个,我们现在可以代入任何x值并将其追溯到预测的y值。这个y值就是x值在某个类中的概率。
06.极大似然估计法Maximum Likelihood Estimation
还记得我们如何通过最小化RSS在线性回归中找到最适合的直线吗?在这里,我们使用所谓的极大似然估计法(MLE)来获得最准确的预测。
MLE通过最能描述我们数据的概率分布参数,得到了最准确的预测。
为什么我们会关心数据的分布?因为它很酷!…但实际上,它只是使我们的数据更易于使用,并使我们的模型可归纳为许多不同的数据。
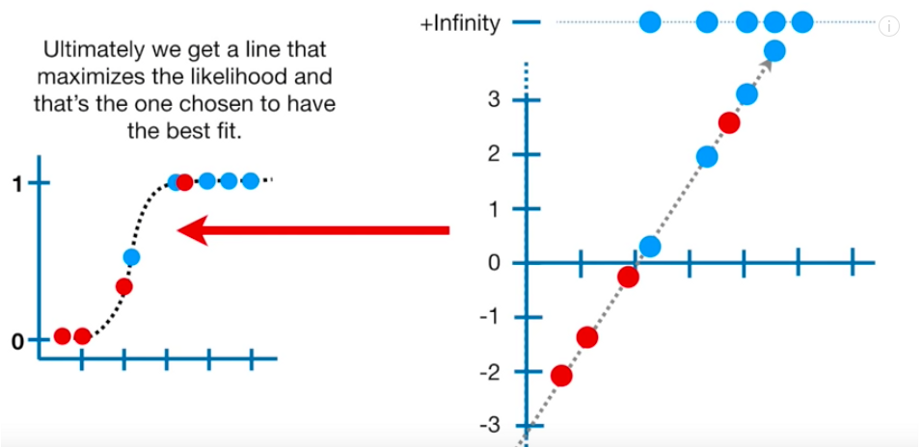
一般情况下,为了得到数据的MLE,我们取s曲线上的数据点并将它们的对数几率相加。基本上,我们想要找到最大化数据对数可能性的s曲线。我们只是不断地计算每个log-odds行(有点像我们对线性回归中每个最佳拟合行的RSS所做的)的log- possibility,直到我们得到最大的数字。
(顺便说一句——我们回到自然对数的世界,因为有时使用对数是最简单的数字形式。这是因为对数是“单调递增”的函数,这基本上意味着它总是递增或递减。我们在MLE过程中得出的估计是那些最大化所谓的“似然函数”的估计(我们在这里不深入讨论)

现在您已经了解了所有关于梯度下降、线性回归和逻辑回归的知识。
接下来,敬请期待第3部分。

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
下一篇
深度学习词汇表(二)
热门企业
热门职位
写评论取消
回复取消






























