从自编码器到变分自编码器(其二)
2018年03月23日 由 yuxiangyu 发表
797172
0
在上一篇介绍自编码器到变分自编码器的文章中,我们讨论了将数据作为输入并发现数据的一些潜在状态表示的模型(欠完备,稀疏,降噪,压缩)。也就是说,我们的输入数据被转换成一个编码向量,其中每个维度表示一些学到的关于数据的属性。在这里,最重要的细节是我们的编码器网络为每个编码维度输出单个值,而解码器网络随后接收这些值并尝试重构原始输入。
变分自编码器(VAE)以概率的方式描述潜在空间观察。因此,我们不会构建一个输出单个值来描述每个潜在状态属性的编码器,而是用编码器来描述每个潜在属性的概率分布。
举一个例子,假设我们在编码维数为6的大型人脸数据集上训练了一个自编码器模型。理想的自编码器将学习人脸的描述性属性,如肤色、是否戴眼镜等,以试图用一些压缩的表示来描述观察。
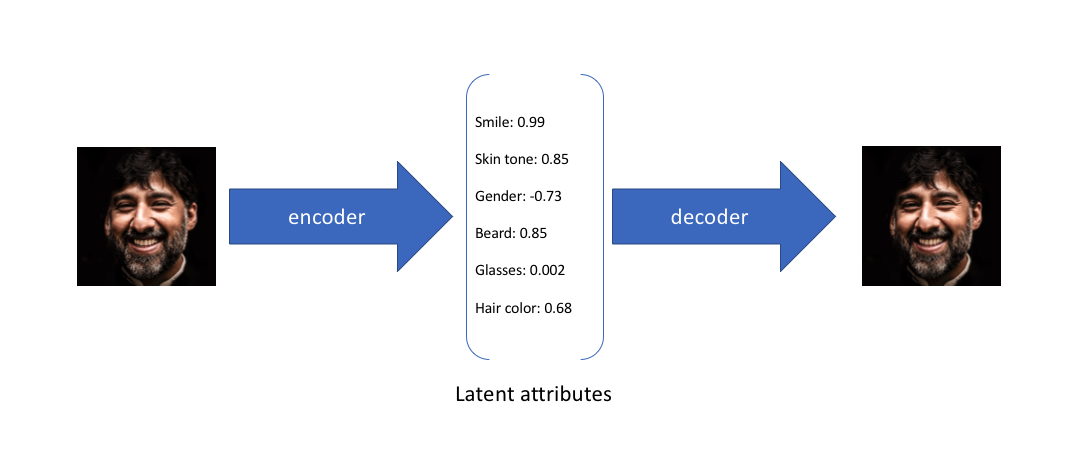
在上面的示例中,我们使用单个值来描述输入图像的潜在属性,以描述每个属性。但我们可能更倾向于将每个潜在属性表示为可能值的范围。例如,如果输入蒙娜丽莎的照片,你会为微笑属性分配什么样的单值?使用变分自编码器,我们可以用概率术语来描述潜在属性。
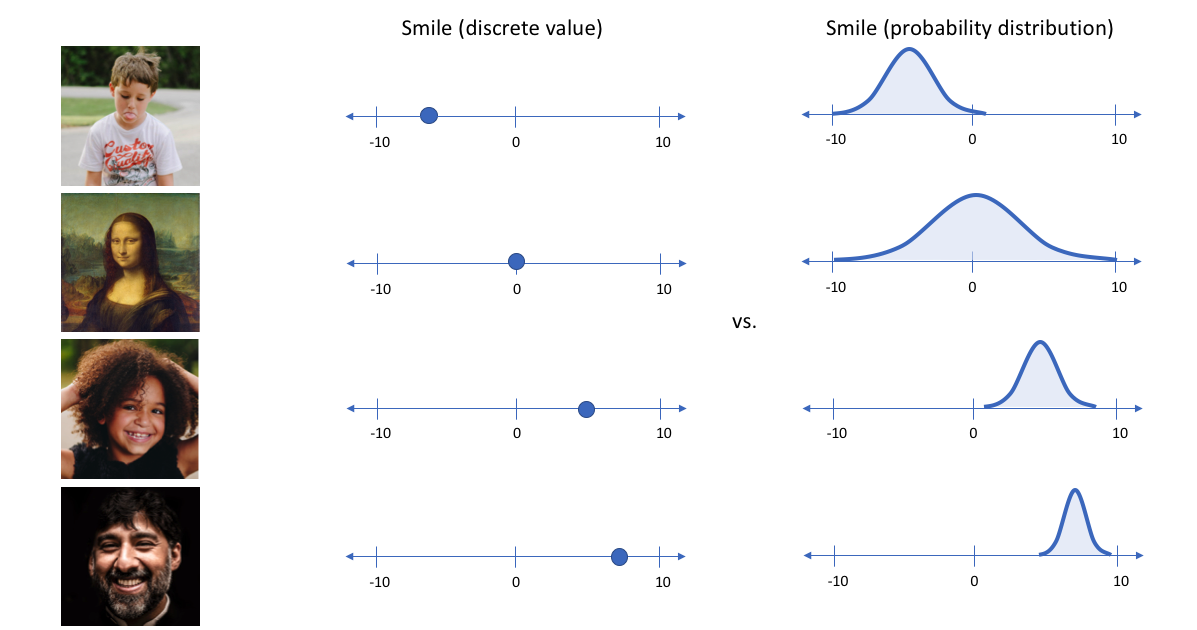
通过这种方法,我们现在将给定输入的每个潜在属性表示为概率分布。当从潜在状态解码时,我们将从每个潜在状态分布中随机采样,生成一个向量作为解码器模型的输入。
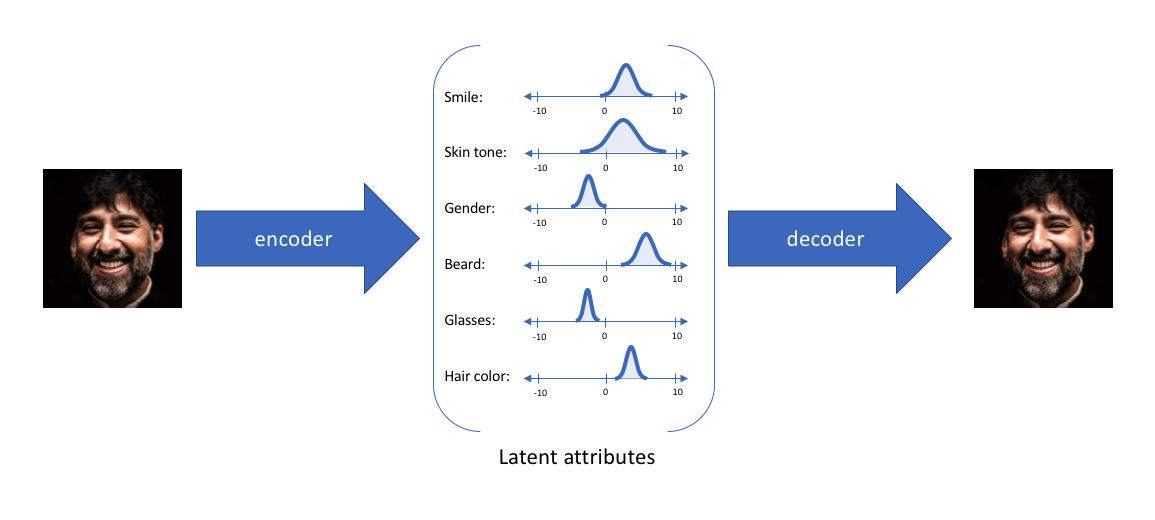
注意:对于变分自编码器,编码器模型有时被称为识别模型(recognition model ),而解码器模型有时被称为生成模型。
通过构造我们的编码器模型来输出可能值的范围(统计分布),我们将随机采样这些值以供给我们的解码器模型,我们实质上实施了连续,平滑的潜在空间表示。对于潜在分布的所有采样,我们期望我们的解码器模型能够准确重构输入。因此,在潜在空间中彼此相邻的值应该与非常类似的重构相对应。
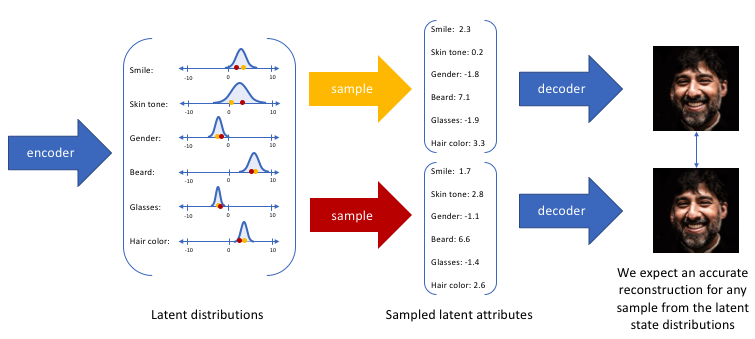
假设存在一些隐藏变量z,生成一个观察x。
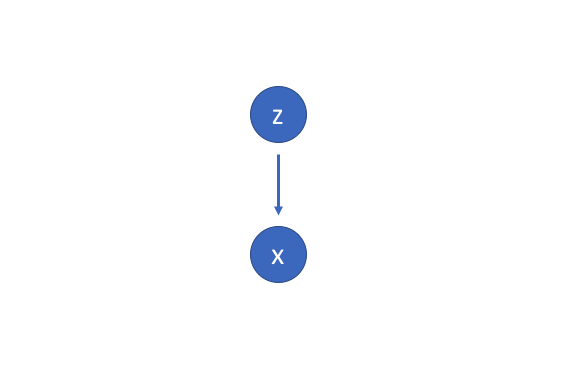
我们只能看到x,但是想推断出z的特征,换句话说,我们想计算p(z|x)
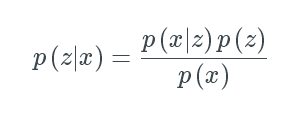
然而,计算p(x)是相当困难的。
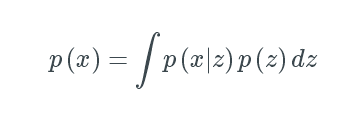
它通常是一个复杂的分布。但是,我们可以应用变分推断( varitational inference)来估计这个值。
让我们用另一个分布q(z|x)来近似p(z|x),我们将定义它具有可伸缩的分布。如果我们可以定义q(z|x)的参数,使其与p(z|x)十分相似,就可以用它来对复杂的分布进行近似的推理。
回想一下,KL散度是两个概率分布的差值。因此,如果我们想要确保q(z|x)与p(z|x)相似,我们可以最小化两个分布之间的KL散度。
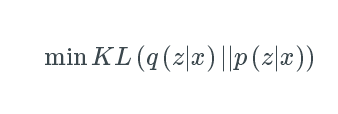
推导出的结果让我们可以通过最大化下面式子的方式最小化上述表达式:
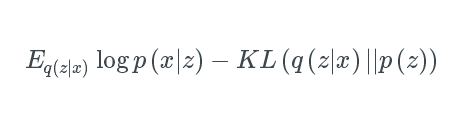
在这里,第一个式子代表重构的可能性,第二个则确保我们学习的分布q类似于真实的先验分布p。
为了重新访问我们的图形模型,我们可以使用q来推断可能隐藏的变量(潜在状态),这些变量可以用于生成观察。我们可以进一步将这个模型构造成神经网络结构,其中编码器模型学习从x到z的映射,解码器模型学习从z到x的映射。
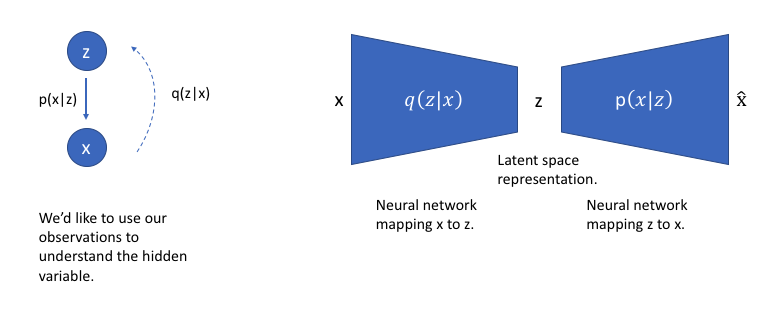
我们网络的损失函数包括两项,第一个惩罚重构误差(可以认为是正如前面所讨论的最大化重构的可能性),第二个鼓励我们学习分布q(z | x)类似于真实的先验分布p(z),我们假设单元高斯分布,每个维度j的潜在空间。
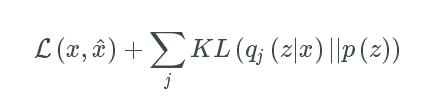
在前面,我建立了变分自编码器结构的统计动机。在本节中,我将提供自己构建这种模型的实际实现细节。
与在标准自编码器中直接输出潜在状态值不同,VAE的编码器模型将输出描述潜在空间中每个维度分布的参数。既然我们假设我们的先验符合正态分布,我们会输出两个向量来描述潜在状态分布的均值和方差。如果我们要构建一个真正的多元高斯模型,我们需要定义一个协方差矩阵来描述每个维度是如何相关的。然而,我们将做一个简化的假设,即我们的协方差矩阵在对角线上只有非零值,允许我们用简单的向量来描述这些信息。
然后,我们的解码器模型将通过从这些已定义的分布中采样,以生成一个潜在矢量,并开始重构原始输入。
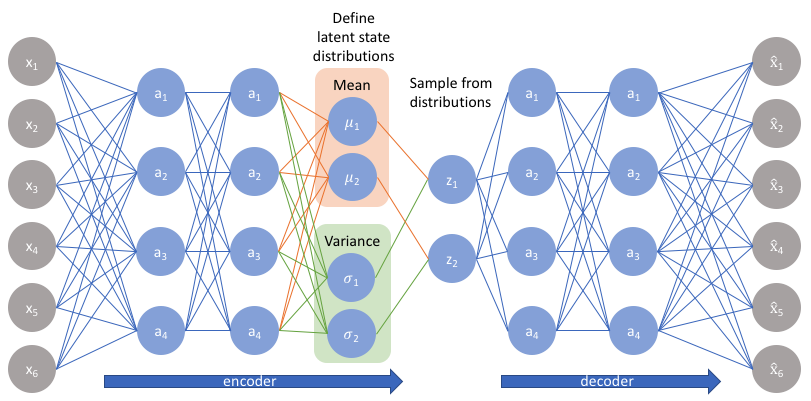
但是,这个采样的过程需要额外注意。在训练模型时,我们需要能够使用反向传播来计算网络中每个参数与最终输出损失之间的关系。但是,我们无法为随机抽样过程做到这一点。幸运的是,我们可以利用一种称为“reparameterization trick”(再参数化)的办法,它暗示我们从单位高斯随机采样ε,然后通过潜在分布的均值μ改变随机采样的ε,最后通过潜在分布的方差σ对其进行缩放。
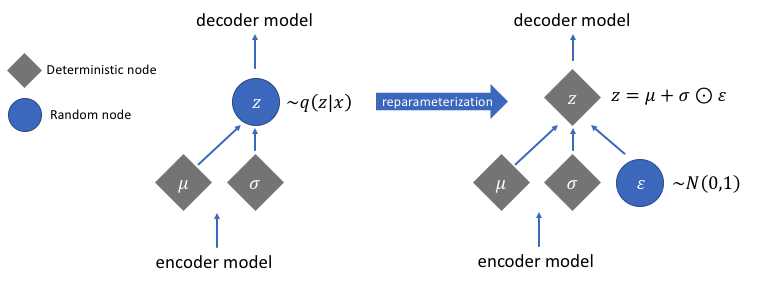
通过这种再参数化,我们现在可以优化分布的参数,同时仍然保持从该分布随机抽样的能力。
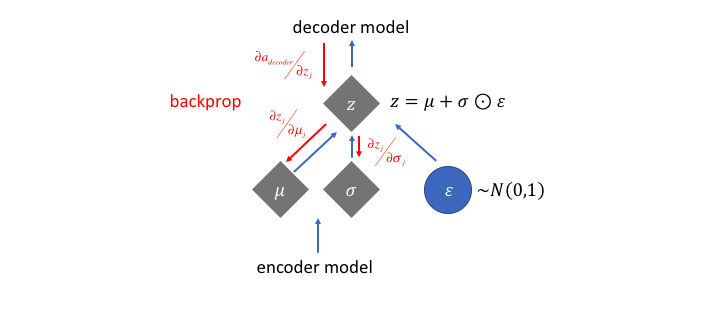
注意:为了应对这一事实网络可以学习σ的负值,我们通常会有网络学习logσ并指数化这个值得到潜在分布的方差。
为了理解变分自编码器模型的含义及它与标准自编码器架构的差异,检查潜在空间很有必要。
变分自编码器的主要优点是我们能够学习输入数据的平滑潜在状态表示。对于标准的自编码器,我们只需要学习一个编码,它允许我们重现输入。如左图所示,只关注重构损失允许我们分离出类(在这种情况下是MNIST数字),这使我们的解码器模型能够重现原始手写数字,但是它的潜在空间内的数据分布不均匀。换句话说,潜在空间中有一些区域不代表我们观测到的任何数据。
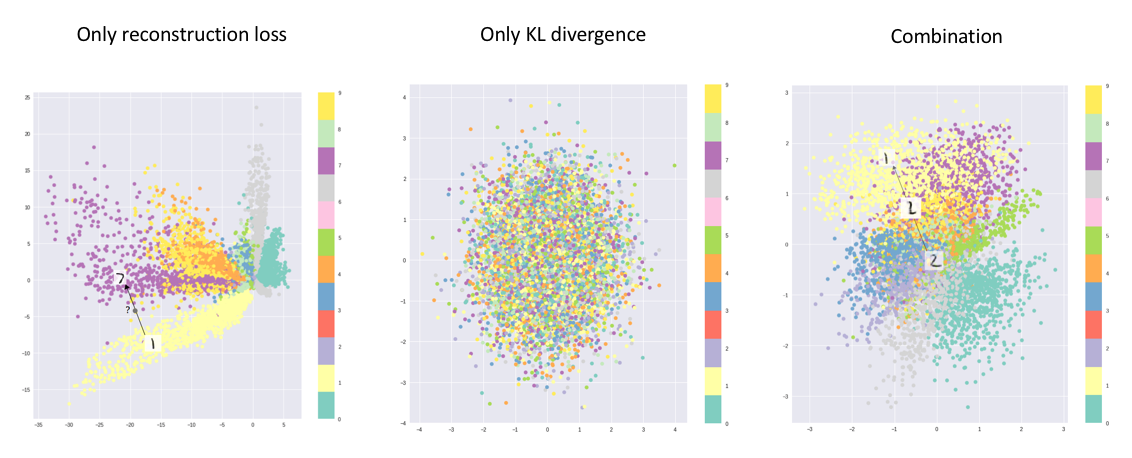
另一方面,如果我们只关注于保持潜在分布与先验分布类似(通过KL散度损失项),我们最终将使用相同的单位高斯描述每个观测值,我们随后从中抽样来描述可视化的潜在维度。这有效地把每一个观察都视为具有相同的特征;换句话说,我们没有描述原始数据。
然而,当这两项同时优化时,我们被鼓励描述一个观察的潜在状态,其分布接近于先验,在必要时偏离,以描述输入的显著特征。
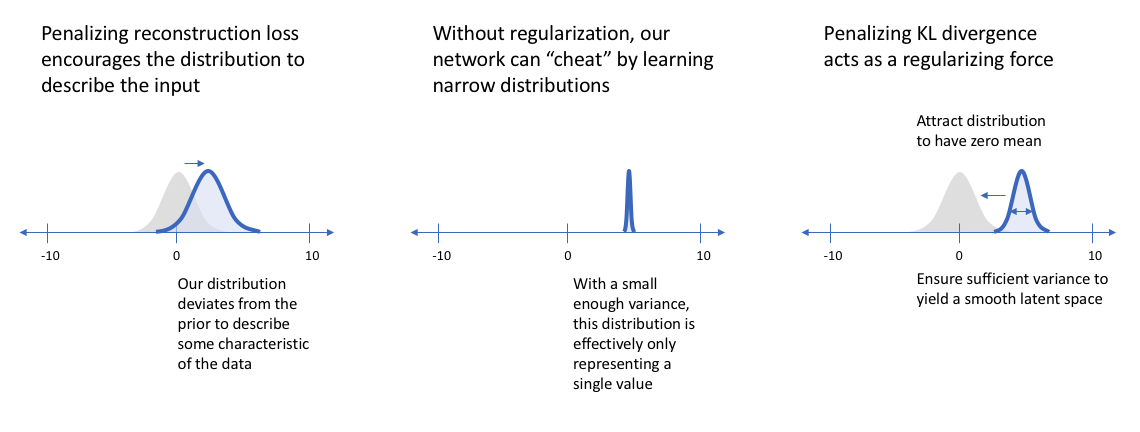
当我构建一个变分自编码器时,我喜欢从数据中检查一些样本的潜在维度,以了解分布的特征。我鼓励你也这样做。
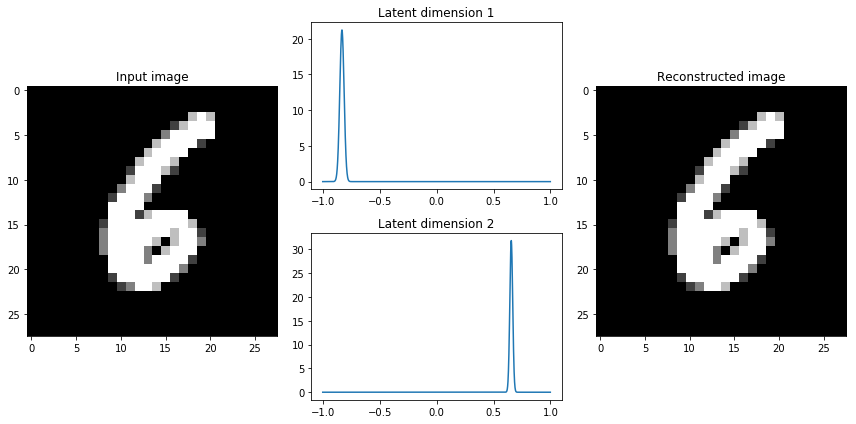
如果我们观察到潜在分布似乎非常密,我们可能需要给参数β> 1的KL散度项赋予更高的权重,鼓励网络学习更广泛的分布。这一简单的见解导致了一种新型的模型 — 解离变分型自动编码器(disentangled variational autoencoders)的增长。事实证明,通过更多的强调KL散度项,我们还隐含地强调学习的潜在维度是不相关的(通过我们对对角协方差矩阵的简化假设)。
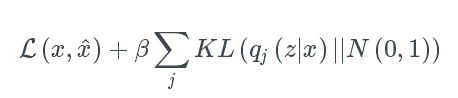
通过从潜在空间采样,我们可以使用解码器网络形成一个生成模型,能够创建与训练过程观察类似的新数据。也就是说,我们将从先验分布p(z)中取样,我们假设它遵循单位高斯分布。
下图显示了训练在MNIST手写数字数据集上的变分自编码器的解码器网络所生成的数据。在这里,我们从二维高斯采样了一个值的网格,并显示解码器网络的输出。

正如你所看到的,每个独立的数字都存在于潜在空间的不同区域,并平滑地从一个数字转换到另一个数字。当你希望在两个观察之间进行插值时,这种平滑的转换非常有用。
变分自编码器(VAE)以概率的方式描述潜在空间观察。因此,我们不会构建一个输出单个值来描述每个潜在状态属性的编码器,而是用编码器来描述每个潜在属性的概率分布。
直觉
举一个例子,假设我们在编码维数为6的大型人脸数据集上训练了一个自编码器模型。理想的自编码器将学习人脸的描述性属性,如肤色、是否戴眼镜等,以试图用一些压缩的表示来描述观察。

在上面的示例中,我们使用单个值来描述输入图像的潜在属性,以描述每个属性。但我们可能更倾向于将每个潜在属性表示为可能值的范围。例如,如果输入蒙娜丽莎的照片,你会为微笑属性分配什么样的单值?使用变分自编码器,我们可以用概率术语来描述潜在属性。

通过这种方法,我们现在将给定输入的每个潜在属性表示为概率分布。当从潜在状态解码时,我们将从每个潜在状态分布中随机采样,生成一个向量作为解码器模型的输入。

注意:对于变分自编码器,编码器模型有时被称为识别模型(recognition model ),而解码器模型有时被称为生成模型。
通过构造我们的编码器模型来输出可能值的范围(统计分布),我们将随机采样这些值以供给我们的解码器模型,我们实质上实施了连续,平滑的潜在空间表示。对于潜在分布的所有采样,我们期望我们的解码器模型能够准确重构输入。因此,在潜在空间中彼此相邻的值应该与非常类似的重构相对应。

统计动机
假设存在一些隐藏变量z,生成一个观察x。

我们只能看到x,但是想推断出z的特征,换句话说,我们想计算p(z|x)
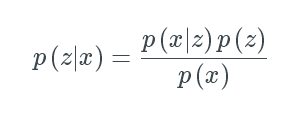
然而,计算p(x)是相当困难的。
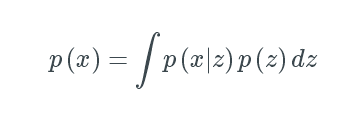
它通常是一个复杂的分布。但是,我们可以应用变分推断( varitational inference)来估计这个值。
让我们用另一个分布q(z|x)来近似p(z|x),我们将定义它具有可伸缩的分布。如果我们可以定义q(z|x)的参数,使其与p(z|x)十分相似,就可以用它来对复杂的分布进行近似的推理。
回想一下,KL散度是两个概率分布的差值。因此,如果我们想要确保q(z|x)与p(z|x)相似,我们可以最小化两个分布之间的KL散度。
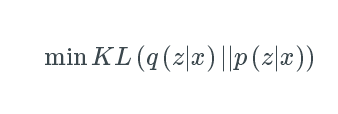
推导出的结果让我们可以通过最大化下面式子的方式最小化上述表达式:
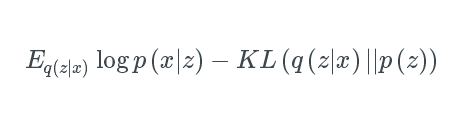
在这里,第一个式子代表重构的可能性,第二个则确保我们学习的分布q类似于真实的先验分布p。
为了重新访问我们的图形模型,我们可以使用q来推断可能隐藏的变量(潜在状态),这些变量可以用于生成观察。我们可以进一步将这个模型构造成神经网络结构,其中编码器模型学习从x到z的映射,解码器模型学习从z到x的映射。

我们网络的损失函数包括两项,第一个惩罚重构误差(可以认为是正如前面所讨论的最大化重构的可能性),第二个鼓励我们学习分布q(z | x)类似于真实的先验分布p(z),我们假设单元高斯分布,每个维度j的潜在空间。
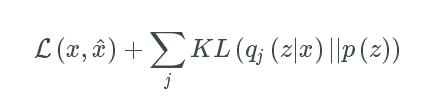
实现
在前面,我建立了变分自编码器结构的统计动机。在本节中,我将提供自己构建这种模型的实际实现细节。
与在标准自编码器中直接输出潜在状态值不同,VAE的编码器模型将输出描述潜在空间中每个维度分布的参数。既然我们假设我们的先验符合正态分布,我们会输出两个向量来描述潜在状态分布的均值和方差。如果我们要构建一个真正的多元高斯模型,我们需要定义一个协方差矩阵来描述每个维度是如何相关的。然而,我们将做一个简化的假设,即我们的协方差矩阵在对角线上只有非零值,允许我们用简单的向量来描述这些信息。
然后,我们的解码器模型将通过从这些已定义的分布中采样,以生成一个潜在矢量,并开始重构原始输入。

但是,这个采样的过程需要额外注意。在训练模型时,我们需要能够使用反向传播来计算网络中每个参数与最终输出损失之间的关系。但是,我们无法为随机抽样过程做到这一点。幸运的是,我们可以利用一种称为“reparameterization trick”(再参数化)的办法,它暗示我们从单位高斯随机采样ε,然后通过潜在分布的均值μ改变随机采样的ε,最后通过潜在分布的方差σ对其进行缩放。

通过这种再参数化,我们现在可以优化分布的参数,同时仍然保持从该分布随机抽样的能力。

注意:为了应对这一事实网络可以学习σ的负值,我们通常会有网络学习logσ并指数化这个值得到潜在分布的方差。
潜在空间的可视化
为了理解变分自编码器模型的含义及它与标准自编码器架构的差异,检查潜在空间很有必要。
变分自编码器的主要优点是我们能够学习输入数据的平滑潜在状态表示。对于标准的自编码器,我们只需要学习一个编码,它允许我们重现输入。如左图所示,只关注重构损失允许我们分离出类(在这种情况下是MNIST数字),这使我们的解码器模型能够重现原始手写数字,但是它的潜在空间内的数据分布不均匀。换句话说,潜在空间中有一些区域不代表我们观测到的任何数据。

另一方面,如果我们只关注于保持潜在分布与先验分布类似(通过KL散度损失项),我们最终将使用相同的单位高斯描述每个观测值,我们随后从中抽样来描述可视化的潜在维度。这有效地把每一个观察都视为具有相同的特征;换句话说,我们没有描述原始数据。
然而,当这两项同时优化时,我们被鼓励描述一个观察的潜在状态,其分布接近于先验,在必要时偏离,以描述输入的显著特征。

当我构建一个变分自编码器时,我喜欢从数据中检查一些样本的潜在维度,以了解分布的特征。我鼓励你也这样做。

如果我们观察到潜在分布似乎非常密,我们可能需要给参数β> 1的KL散度项赋予更高的权重,鼓励网络学习更广泛的分布。这一简单的见解导致了一种新型的模型 — 解离变分型自动编码器(disentangled variational autoencoders)的增长。事实证明,通过更多的强调KL散度项,我们还隐含地强调学习的潜在维度是不相关的(通过我们对对角协方差矩阵的简化假设)。
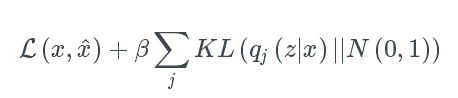
变分自编码器作为生成模型
通过从潜在空间采样,我们可以使用解码器网络形成一个生成模型,能够创建与训练过程观察类似的新数据。也就是说,我们将从先验分布p(z)中取样,我们假设它遵循单位高斯分布。
下图显示了训练在MNIST手写数字数据集上的变分自编码器的解码器网络所生成的数据。在这里,我们从二维高斯采样了一个值的网格,并显示解码器网络的输出。

正如你所看到的,每个独立的数字都存在于潜在空间的不同区域,并平滑地从一个数字转换到另一个数字。当你希望在两个观察之间进行插值时,这种平滑的转换非常有用。

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
热门企业
热门职位
写评论取消
回复取消






























