在执行数据科学（DS）时，统计是一种强大的工具。笼统来看，统计学是利用数学来进行数据的技术分析。基础的可视化（例如，条形图等）可能会为你提供一些高级信息，而通过统计，我们可以以更加信息驱动且更有针对性的方式对数据进行操作。当中用到的数学帮助我们形成关于我们数据的具体结论，而不仅仅是猜测。

使用统计数据，我们可以获得更深入，更细致的了解我们的数据是如何构建的，并且可以知道基于该结构，我们如何最好地应用其他数据科学技术来获取更多信息。现在，我们来看看数据科学家需要了解的5个基本统计概念以及如何最有效地应用它们！

统计特征

统计特征可能是数据科学中最常用的统计概念。它通常是你在探索数据集时应用的第一种统计技术，包括偏差（bias），方差，均值，中位数，百分位数等等。在代码中理解和实现都非常容易！

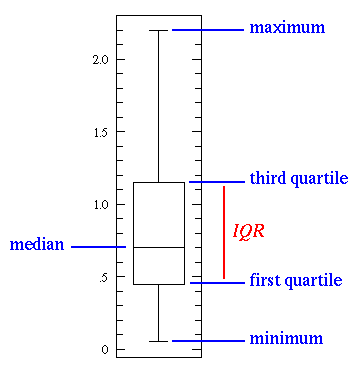
箱形图（也称为盒须图）

中值的线是数据的中位数（median ）。由于中位数对离群值的鲁棒性更强，因此中位数要比均值更常用。第一个四分位数（first quartile）基本上是第25个百分位，即数据中25％的点低于该值。第三个四分位数（third quartile）是第75百分位，即数据中75％的点低于该值。最小值和最大值表示数据范围的上端和下端。

箱形图完美地说明了我们可以用基本统计特征做什么：

• 当箱形图很短时，它意味着大部分数据点都相似，因为大多数值在在很小的范围内


• 当箱形图很高时，它意味着大部分数据点都非常不同，因为这些值分布在很广的范围内


• 如果中值接近底部，那么我们知道大多数数据具有较低的值。如果中值接近顶部，那么我们知道大多数数据具有更高的值。基本上，如果中值的线不在框的中间，则表明数据偏斜。


• 须很长吗（whisker，指盒的延长线）？这意味着数据具有较高的标准偏差和方差，即数值分散且变化很大。如果盒子的一侧有须，而另一侧没有，那么你的数据可能只在一个方向上变化很大。

所有这些信息来自一些易于计算的简单统计特征！只要你需要快速而翔实的数据视图，请尝试这些。

概率分布

我们可以将概率定义为某个事件发生的几率。在数据科学中，通常被量化在0到1之间，0表示我们确信这不会发生，1表示我们确信它会发生。另外，概率分布是表示实验中所有可能值概率的函数。如下图：

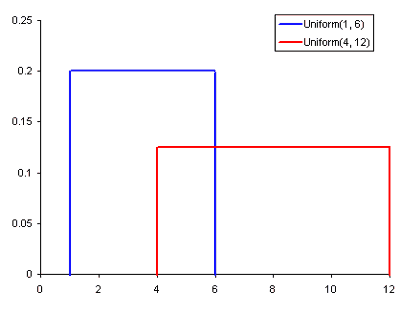
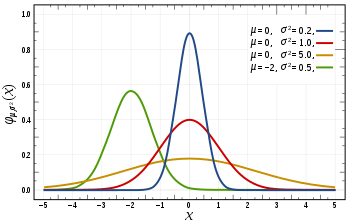
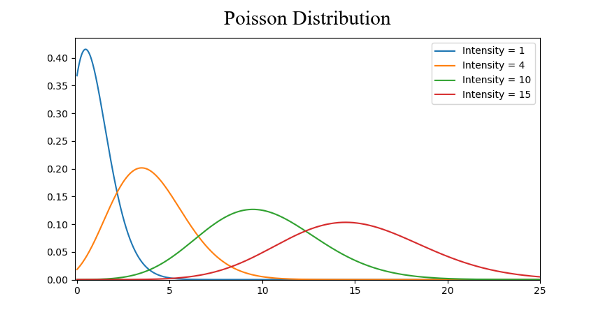
常见的概率分布，依次为均匀分布，正态分布，泊松分布

• 均匀分布是三个中最基础的。它在一定范围内只有单个值，而超出该范围这值为0。这可以视为一个开/关分布。也可以把它看作是一个有两个类别的分类变量:0或值。你的分类变量可能有多个非0的值，但我们仍然可以将其视为多个均匀分布的分段函数。


• 正态分布通常被称为高斯分布，具体由它的均值和标准差定义。均值在改变分布空间，标准差控制离散。与其他分布（例如泊松）的主要区别在于标准差在所有方向上是相同的。因此，利用高斯分布，我们知道数据集的均值以及数据的离散，即它是在很大范围内离散还是高度集中在几个值附近。


• 一个泊松分布类似于正态分布，但增加了偏度。偏度值较低时，泊松分布将在所有方向上具有相对均匀分布，就像正态分布一样。但是当偏度值的较大时，我们的数据在不同方向上的分布会有所不同，在一个方向上它将非常分散，而在另一个方向上它将高度集中。

你可以深入研究更多的分布，但这几种分布已经给了我们很多有价值的线索。我们可以使用均匀分布快速查看和解释我们的分类变量。如果我们看到高斯分布，我们知道有许多算法默认情况下会特别适用于高斯分布，所以我们应该使用这样的算法。使用泊松分布，我们必须很小心地选择一种对空间分布具有鲁棒性的算法。

降维

降维这个术语很容易理解。我们有一个数据集，我们想减少它的维度数。在数据科学中，维度数是特征变量的数量。如下图：

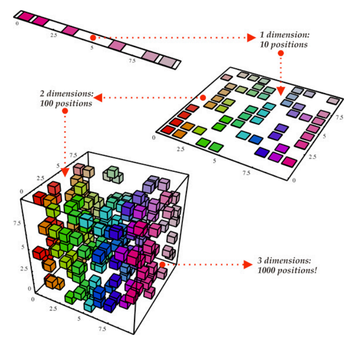
降维

立方体表示我们的数据集，它有3个维度，总共1000个点。现在，计算1000点很容易处理，但如果有更大的规模，我们会遇到问题。然而，仅从二维视角（例如从立方体的一侧）查看我们的数据，我们就可以看到从该角度划分这些颜色非常容易。通过降维，我们可以将三维数据投射到二维平面上。这有效地将我们需要计算的点数从1000减少到100，大大节省了计算量！

我们也可以通过特征剪枝来降低维数。通过特征剪枝，我们基本上可以删除任何我们认为对我们的分析不重要的特征。例如，在研究数据集之后，我们可能会发现，在10个特征中，有7个与输出高度相关，而其他3个具有的相关性非常低。那么，这3个特征可能不值得计算，我们也许可以从我们的分析中删除它们，且不会影响输出。

用于降维的最常见的统计技术是PCA，它基本上创建了特征的向量表示以显示了它们对输出的重要性（(即它们的相关性)）。PCA可用于执行上面讨论的两种降维方式。

过采样和欠采样

过采样和欠采样是用于分类问题的技术。有时，我们的分类数据集可能会过于倾斜于某一边。例如，我们在类1中有2000个实例，而在类2中只有200个。它可以迷惑许多我们尝试和使用进行建模数据和作出预测的机器学习技术！而过采样和欠采样可以解决这个问题。如下图：

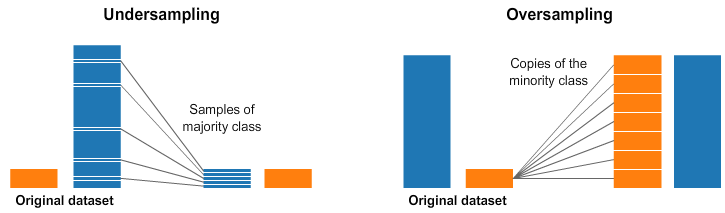
在上图中，我们的蓝色类比橙色类有更多的样本。在这种情况下，我们有两个预处理选项可以帮助我们的机器学习模型的训练。

欠采样的意思是，我们将只选择多数类中的一部分数据，而使用少数类中尽可能多的实例。这个选择需要保持类的概率分布。这很简单，只需少量样本就可以使我们的数据集保持平衡！

过采样的意思是，我们创建我们的少数类的副本，以便拥有与多数类相同数量的实例。制作副本，以维持少数类的分布。我们是在没有获得更多数据的情况下平衡了我们的数据集！

贝叶斯统计

完全理解我们使用贝叶斯统计的原因要求我们首先了解频率统计（ Frequency Statistics）失败的地方。频率统计是大多数人在听到“概率”一词时所想到的统计数据类型。它涉及应用数学来分析某些事件发生的概率，即，我们计算的唯一数据是先验数据。

我们来看一个例子。假设我给了你一个骰子然后问你掷出6的概率是多少。大多数人会说它是1 / 6。事实上，如果我们要进行频率分析，我们会看有人滚动10,000次骰子，然后计算每个数字的频率，它大概是1/6！

但是，如果有人告诉你，我们给你的是特殊的骰子，结果总是落在6上呢？由于频率分析只解释以前的数据，分析给你的骰子被动过手脚的证据没有被考虑在内。

贝叶斯统计确实考虑了这一证据。我们可以用贝叶斯定理来说明这一点：

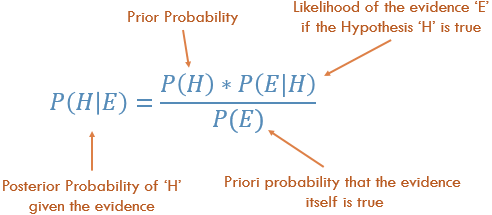
我们公式中的概率P（H）是我们的频率分析，根据我们之前的数据，我们这个事件发生的可能性是多少。根据我们频率分析的信息，我们方程中的P（E | H）被称为似然性（likelihood），本质上是我们的证明是正确的概率。例如，如果你想要将骰子滚动10,000次，而前1000次滚动你得到的全部是6，你就会开始相信这个骰子被动了手脚！P(E)是实际证据成立的概率。如果我告诉你骰子被动手脚了，你能相信我并说它确实被动手脚了，而不是认为我在骗你！

如果我们的频率分析非常好，那么它就会有一定的权重来表示我们对6的猜测是正确的。同时，我们将之视为我们改装骰子的证据，如果它为真或不基于它自己的先验和频率分析。从方程式可以看出，贝叶斯统计将一切都考虑在内，只要你认为先前的数据不能很好地代表你未来的数据和结果，就可以使用它。