一个简单而强大的深度学习库—PyTorch入门介绍
2018年03月04日 由 yuxiangyu 发表
863940
0
每过一段时间,总会有一个python库被开发出来,改变深度学习领域。而PyTorch就是这样一个库。
在过去的几周里,我一直在尝试使用PyTorch。我发现它非常好上手。迄今为止,在我所有的各种深度学习库中,PyTorch一直是最灵活和容易的。

在本文中,我们将探索PyTorch的实际应用,其中包括基础知识和案例研究。我们还将比较使用numpy和PyTorch构建的神经网络,以查看它们在实现中的相似之处。
PyTorch的创作者说他们信奉的道理是 - 解决当务之急。这意味着我们立即运行我们的计算。这恰好适合python的编程方法,因为我们不必等待所有代码都写完才能知道它是否有效。我们可以运行部分代码并实时检查它。对于我,一个神经网络调试器来说,这无意是一个福音!
PyTorch是一个基于python的库,旨在提供灵活的深度学习开发平台。PyTorch的工作流程很可能接近python的科学计算库 - numpy。
那么,为什么我们要使用PyTorch来构建深度学习模型?:
使用PyTorch的还有其他的优点,它能够支持multiGPU,自定义数据加载和简化的预处理程序。
自2016年1月初发布以来,许多研究人员已将其作为一种实现库,因为它易于构建新颖甚至非常复杂的计算图。话虽如此,PyTorch仍然需要一段时间才能被大多数数据科学从业者所采用,因为它是新的并且正在建设中。
在深入细节之前,让我们了解PyTorch的工作流程。
PyTorch使用命令式/热切式范式。也就是说,构建图形的每行代码都定义了该图的一个组件。即使在图形完全构建之前,我们也可以独立地对这些组件进行计算。这被称为运行时定义(define-by-run)法。

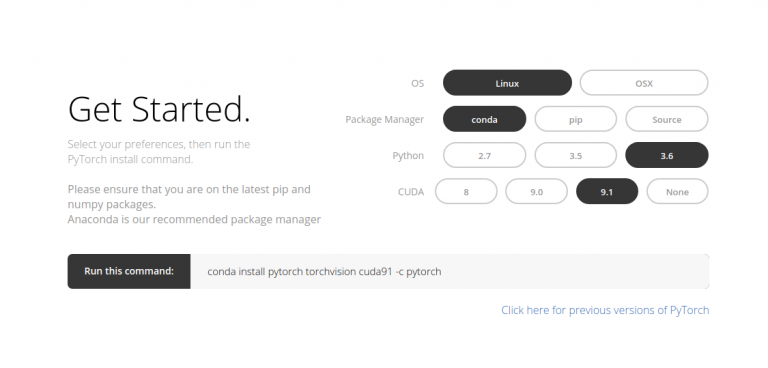
安装PyTorch非常简单。您可以按照它的官方文档操作,并根据自己的系统规格运行命令。例如,下面是我根据我的情况使用的命令:
我们在开始使用PyTorch时应该了解的主要元素是:
张量不过是多维数组。PyTorch中的张量与numpy的ndarray相似,张量也可以在GPU上使用。PyTorch支持很多类型的张量。
你可以定义一个简单的一维矩阵如下:
与numpy一样,科学计算库需要高效的实现数学函数。PyTorch提供了一个相似的接口,可以使用超过200多种数学运算。
以下是PyTorch中一个简单加法操作的例子:
这看起来不像是一种quinessential python方法吗?我们也可以对我们定义的PyTorch张量执行各种矩阵运算。例如,我们将转置一个二维矩阵:
PyTorch使用一种称为自动微分(automatic differentiation)的技术。也就是说,有一个记录我们所执行的操作的记录器,然后它会反向回放以计算我们的梯度。这种技术在建立神经网络时尤为有效,因为我们可以通过计算正向传递过程中参数的微分来节省一个周期的时间。
torch.optim 是一个实现构建神经网络的各种优化算法的模块。大多数常用的方法已经被支持,因此我们不必从头开始构建它们(除非你乐意这么做)。
以下是使用Adam优化的代码:
PyTorch的autograd模块可以很容易地定义计算图和梯度,但是默认的autograd对于定义复杂的神经网络可能有些低级。这时就要用到nn模块。
nn包定义了一组模块,我们可以将其视为一个神经网络层,它可以从输入生成输出,并且具有一些可训练的权重。
您可以将一个nn模块视为PyTorch 的keras!
我之前提到PyTorch和Numpy非常相似。那么,我们来看看为什么,一个简单的神经网络的实现来解决二元分类问题。使用Numpy如下:
使用PyTorch如下(下面的代码中用粗体表示差异):
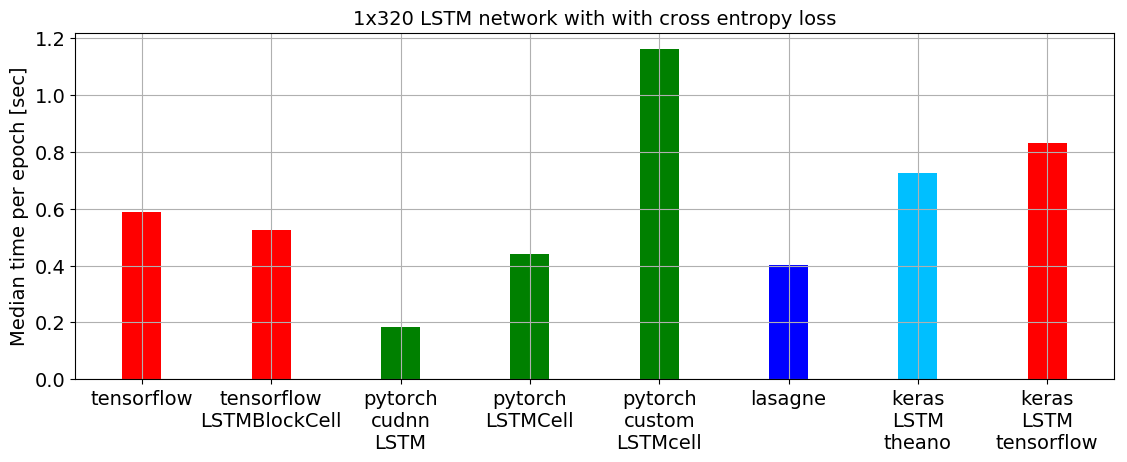
在一个基准脚本中,PyTorch 在训练LSTM方面表现优于所有其他主要的深度学习库,每个周期的中位时间最低(参见下图)。
在PyTorch中用于数据加载的API设计良好。接口在数据集,采样器和数据加载器中指定。
在比较TensorFlow中的数据加载工具(readers,queues,等)时,我发现PyTorch的数据加载模块非常好用。另外,PyTorch可以无缝的构建神经网络,我们不必依赖像keras这样的第三方高级库。
另一方面,我不会推荐使用PyTorch进行部署。PyTorch还在发展中。正如PyTorch开发人员所说:“我们看到的是,用户首先创建了一个PyTorch模型。当他们准备将他们的模型部署到生产环境中时,他们只需将其转换为Caffe 2模型,然后将其发布到移动平台或其他平台中。“
为了熟悉PyTorch,我们将解决分析方面的深度学习实践问题 - 识别数字。
我们的要做的是一个图像识别问题,从一个给定的28×28像素的图像中识别数字。我们有一部分图像用于训练,其余部分用于测试我们的模型。
首先,下载训练集与测试集。数据集包含所有图像的压缩文件,并且train.csv和test.csv都具有相应训练和测试图像的名称。数据集中不提供任何额外特征,图片为.png格式。
a)导入所有需要用到的库
b)让我们设置seed值,以便我们可以控制模型的随机性
c)第一步是设置目录路径,以便妥善保存!
a)现在让我们读取数据集。
b)让我们看看我们的数据是什么样的。我们阅读我们的图像并显示它。
d)为了便于数据处理,让我们将所有图像存储为numpy数组
e)这是一个典型的机器学习问题,为了测试我们模型的是否正常运行,我们创建一个验证集。我们分离他们的比例为70:30(验证集为30)。
a)下面,我们定义神经网络架构。我们定义了一个3个层(输入,隐藏和输出)的神经网络。输入和输出中神经元的数量是固定的,因为输入是我们图像28×28,并且输出是代表类的10×1向量(即每个像素对应一个输入神经元,每个类为一个输出)。我们在隐藏层中采用50个神经元。在这里,我们使用Adam作为我们的优化算法,它是梯度下降算法的一个不错的变种。
b)训练模型
训练分数是:
验证分数是:
这个分数相当的高,我们才训练这个简单的神经网络五个周期而已。
在过去的几周里,我一直在尝试使用PyTorch。我发现它非常好上手。迄今为止,在我所有的各种深度学习库中,PyTorch一直是最灵活和容易的。

在本文中,我们将探索PyTorch的实际应用,其中包括基础知识和案例研究。我们还将比较使用numpy和PyTorch构建的神经网络,以查看它们在实现中的相似之处。
PyTorch概述
PyTorch的创作者说他们信奉的道理是 - 解决当务之急。这意味着我们立即运行我们的计算。这恰好适合python的编程方法,因为我们不必等待所有代码都写完才能知道它是否有效。我们可以运行部分代码并实时检查它。对于我,一个神经网络调试器来说,这无意是一个福音!
PyTorch是一个基于python的库,旨在提供灵活的深度学习开发平台。PyTorch的工作流程很可能接近python的科学计算库 - numpy。
那么,为什么我们要使用PyTorch来构建深度学习模型?:
- 易于使用的API - 如Python一样简单。
- Python支持 - 如上所述,PyTorch平滑地与Python数据科学堆栈结合。它与numpy非常相似,你甚至很难注意到他们的差异。
- 动态计算图 - PyTorch并没有为特定功能预定义图形,而是为我们提供了一个框架,可以随时随地构建计算图,甚至在运行时更改计算图。我们不知道创建一个神经网络需要多少内存时,这非常有用。
使用PyTorch的还有其他的优点,它能够支持multiGPU,自定义数据加载和简化的预处理程序。
自2016年1月初发布以来,许多研究人员已将其作为一种实现库,因为它易于构建新颖甚至非常复杂的计算图。话虽如此,PyTorch仍然需要一段时间才能被大多数数据科学从业者所采用,因为它是新的并且正在建设中。
在深入细节之前,让我们了解PyTorch的工作流程。
PyTorch使用命令式/热切式范式。也就是说,构建图形的每行代码都定义了该图的一个组件。即使在图形完全构建之前,我们也可以独立地对这些组件进行计算。这被称为运行时定义(define-by-run)法。

安装PyTorch非常简单。您可以按照它的官方文档操作,并根据自己的系统规格运行命令。例如,下面是我根据我的情况使用的命令:

conda install pytorch torchvision cuda91 -c pytorch
我们在开始使用PyTorch时应该了解的主要元素是:
- PyTorch张量
- 数学运算
- Autograd模块
- Optim模块
- nn模块
PyTorch张量
张量不过是多维数组。PyTorch中的张量与numpy的ndarray相似,张量也可以在GPU上使用。PyTorch支持很多类型的张量。
你可以定义一个简单的一维矩阵如下:
# import pytorch
import torch
# define a tensor
torch.FloatTensor([2])
2
[torch.FloatTensor of size 1]
数学运算
与numpy一样,科学计算库需要高效的实现数学函数。PyTorch提供了一个相似的接口,可以使用超过200多种数学运算。
以下是PyTorch中一个简单加法操作的例子:
a = torch.FloatTensor([2])
b = torch.FloatTensor([3])
a + b
5
[torch.FloatTensor of size 1]
这看起来不像是一种quinessential python方法吗?我们也可以对我们定义的PyTorch张量执行各种矩阵运算。例如,我们将转置一个二维矩阵:
matrix = torch.randn(3, 3)
matrix
-1.3531 -0.5394 0.8934
1.7457 -0.6291 -0.0484
-1.3502 -0.6439 -1.5652
[torch.FloatTensor of size 3x3]
matrix.t()
-2.1139 1.8278 0.1976
0.6236 0.3525 0.2660
-1.4604 0.8982 0.0428
[torch.FloatTensor of size 3x3]
Autograd模块
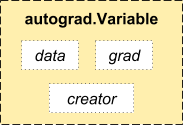
PyTorch使用一种称为自动微分(automatic differentiation)的技术。也就是说,有一个记录我们所执行的操作的记录器,然后它会反向回放以计算我们的梯度。这种技术在建立神经网络时尤为有效,因为我们可以通过计算正向传递过程中参数的微分来节省一个周期的时间。

from torch.autograd import Variable
x = Variable(train_x)
y = Variable(train_y, requires_grad=False)
Optim模块
torch.optim 是一个实现构建神经网络的各种优化算法的模块。大多数常用的方法已经被支持,因此我们不必从头开始构建它们(除非你乐意这么做)。
以下是使用Adam优化的代码:
optimizer = torch.optim.Adam(model.parameters(),lr = learning_rate)
nn模块
PyTorch的autograd模块可以很容易地定义计算图和梯度,但是默认的autograd对于定义复杂的神经网络可能有些低级。这时就要用到nn模块。
nn包定义了一组模块,我们可以将其视为一个神经网络层,它可以从输入生成输出,并且具有一些可训练的权重。
您可以将一个nn模块视为PyTorch 的keras!
import torch
# define model
model = torch.nn.Sequential(
torch.nn.Linear(input_num_units, hidden_num_units),
torch.nn.ReLU(),
torch.nn.Linear(hidden_num_units, output_num_units),
)
loss_fn = torch.nn.CrossEntropyLoss()
在Numpy与PyTorch建立一个神经网络的对比
我之前提到PyTorch和Numpy非常相似。那么,我们来看看为什么,一个简单的神经网络的实现来解决二元分类问题。使用Numpy如下:
## Neural network in numpy
import numpy as np
#Input array
X=np.array([[1,0,1,0],[1,0,1,1],[0,1,0,1]])
#Output
y=np.array([[1],[1],[0]])
#Sigmoid Function
def sigmoid (x):
return 1/(1 + np.exp(-x))
#Derivative of Sigmoid Function
def derivatives_sigmoid(x):
return x * (1 - x)
#Variable initialization
epoch=5000 #Setting training iterations
lr=0.1 #Setting learning rate
inputlayer_neurons = X.shape[1] #number of features in data set
hiddenlayer_neurons = 3 #number of hidden layers neurons
output_neurons = 1 #number of neurons at output layer
#weight and bias initialization
wh=np.random.uniform(size=(inputlayer_neurons,hiddenlayer_neurons))
bh=np.random.uniform(size=(1,hiddenlayer_neurons))
wout=np.random.uniform(size=(hiddenlayer_neurons,output_neurons))
bout=np.random.uniform(size=(1,output_neurons))
for i in range(epoch):
#Forward Propogation
hidden_layer_input1=np.dot(X,wh)
hidden_layer_input=hidden_layer_input1 + bh
hiddenlayer_activations = sigmoid(hidden_layer_input)
output_layer_input1=np.dot(hiddenlayer_activations,wout)
output_layer_input= output_layer_input1+ bout
output = sigmoid(output_layer_input)
#Backpropagation
E = y-output
slope_output_layer = derivatives_sigmoid(output)
slope_hidden_layer = derivatives_sigmoid(hiddenlayer_activations)
d_output = E * slope_output_layer
Error_at_hidden_layer = d_output.dot(wout.T)
d_hiddenlayer = Error_at_hidden_layer * slope_hidden_layer
wout += hiddenlayer_activations.T.dot(d_output) *lr
bout += np.sum(d_output, axis=0,keepdims=True) *lr
wh += X.T.dot(d_hiddenlayer) *lr
bh += np.sum(d_hiddenlayer, axis=0,keepdims=True) *lr
print('actual :\n', y, '\n')
print('predicted :\n', output)
使用PyTorch如下(下面的代码中用粗体表示差异):
## neural network in pytorch
import torch
#Input array
X = torch.Tensor([[1,0,1,0],[1,0,1,1],[0,1,0,1]])
#Output
y = torch.Tensor([[1],[1],[0]])
#Sigmoid Function
def sigmoid (x):
return 1/(1 + torch.exp(-x))
#Derivative of Sigmoid Function
def derivatives_sigmoid(x):
return x * (1 - x)
#Variable initialization
epoch=5000 #Setting training iterations
lr=0.1 #Setting learning rate
inputlayer_neurons = X.shape[1] #number of features in data set
hiddenlayer_neurons = 3 #number of hidden layers neurons
output_neurons = 1 #number of neurons at output layer
#weight and bias initialization
wh=torch.randn(inputlayer_neurons, hiddenlayer_neurons).type(torch.FloatTensor)
bh=torch.randn(1, hiddenlayer_neurons).type(torch.FloatTensor)
wout=torch.randn(hiddenlayer_neurons, output_neurons)
bout=torch.randn(1, output_neurons)
for i in range(epoch):
#Forward Propogation
hidden_layer_input1 = torch.mm(X, wh)
hidden_layer_input = hidden_layer_input1 + bh
hidden_layer_activations = sigmoid(hidden_layer_input)
output_layer_input1 = torch.mm(hidden_layer_activations, wout)
output_layer_input = output_layer_input1 + bout
output = sigmoid(output_layer_input1)
#Backpropagation
E = y-output
slope_output_layer = derivatives_sigmoid(output)
slope_hidden_layer = derivatives_sigmoid(hidden_layer_activations)
d_output = E * slope_output_layer
Error_at_hidden_layer = torch.mm(d_output, wout.t())
d_hiddenlayer = Error_at_hidden_layer * slope_hidden_layer
wout += torch.mm(hidden_layer_activations.t(), d_output) *lr
bout += d_output.sum() *lr
wh += torch.mm(X.t(), d_hiddenlayer) *lr
bh += d_output.sum() *lr
print('actual :\n', y, '\n')
print('predicted :\n', output)
与其他深度学习库比较
在一个基准脚本中,PyTorch 在训练LSTM方面表现优于所有其他主要的深度学习库,每个周期的中位时间最低(参见下图)。

在PyTorch中用于数据加载的API设计良好。接口在数据集,采样器和数据加载器中指定。
在比较TensorFlow中的数据加载工具(readers,queues,等)时,我发现PyTorch的数据加载模块非常好用。另外,PyTorch可以无缝的构建神经网络,我们不必依赖像keras这样的第三方高级库。
另一方面,我不会推荐使用PyTorch进行部署。PyTorch还在发展中。正如PyTorch开发人员所说:“我们看到的是,用户首先创建了一个PyTorch模型。当他们准备将他们的模型部署到生产环境中时,他们只需将其转换为Caffe 2模型,然后将其发布到移动平台或其他平台中。“
案例研究 - 解决PyTorch中的图像识别问题
为了熟悉PyTorch,我们将解决分析方面的深度学习实践问题 - 识别数字。
我们的要做的是一个图像识别问题,从一个给定的28×28像素的图像中识别数字。我们有一部分图像用于训练,其余部分用于测试我们的模型。
首先,下载训练集与测试集。数据集包含所有图像的压缩文件,并且train.csv和test.csv都具有相应训练和测试图像的名称。数据集中不提供任何额外特征,图片为.png格式。
第0步:准备工作
a)导入所有需要用到的库
# import modules
%pylab inline
import os
import numpy as np
import pandas as pd
from scipy.misc import imread
from sklearn.metrics import accuracy_score
b)让我们设置seed值,以便我们可以控制模型的随机性
# To stop potential randomness
seed = 128
rng = np.random.RandomState(seed)
c)第一步是设置目录路径,以便妥善保存!
root_dir = os.path.abspath('.')
data_dir = os.path.join(root_dir, 'data')
# check for existence
os.path.exists(root_dir), os.path.exists(data_dir)第1步:数据加载和预处理
a)现在让我们读取数据集。
# load dataset
train = pd.read_csv(os.path.join(data_dir, 'Train', 'train.csv'))
test = pd.read_csv(os.path.join(data_dir, 'Test.csv'))
sample_submission = pd.read_csv(os.path.join(data_dir, 'Sample_Submission.csv'))
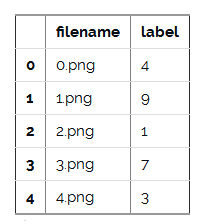
train.head()

b)让我们看看我们的数据是什么样的。我们阅读我们的图像并显示它。
# print an image
img_name = rng.choice(train.filename)
filepath = os.path.join(data_dir, 'Train', 'Images', 'train', img_name)
img = imread(filepath, flatten=True)
pylab.imshow(img, cmap='gray')
pylab.axis('off')
pylab.show()
d)为了便于数据处理,让我们将所有图像存储为numpy数组
# load images to create train and test set
temp = []
for img_name in train.filename:
image_path = os.path.join(data_dir, 'Train', 'Images', 'train', img_name)
img = imread(image_path, flatten=True)
img = img.astype('float32')
temp.append(img)
train_x = np.stack(temp)
train_x /= 255.0
train_x = train_x.reshape(-1, 784).astype('float32')
temp = []
for img_name in test.filename:
image_path = os.path.join(data_dir, 'Train', 'Images', 'test', img_name)
img = imread(image_path, flatten=True)
img = img.astype('float32')
temp.append(img)
test_x = np.stack(temp)
test_x /= 255.0
test_x = test_x.reshape(-1, 784).astype('float32')
train_y = train.label.values
e)这是一个典型的机器学习问题,为了测试我们模型的是否正常运行,我们创建一个验证集。我们分离他们的比例为70:30(验证集为30)。
# create validation set
split_size = int(train_x.shape[0]*0.7)
train_x, val_x = train_x[:split_size], train_x[split_size:]
train_y, val_y = train_y[:split_size], train_y[split_size:]
第2步:建立模型
a)下面,我们定义神经网络架构。我们定义了一个3个层(输入,隐藏和输出)的神经网络。输入和输出中神经元的数量是固定的,因为输入是我们图像28×28,并且输出是代表类的10×1向量(即每个像素对应一个输入神经元,每个类为一个输出)。我们在隐藏层中采用50个神经元。在这里,我们使用Adam作为我们的优化算法,它是梯度下降算法的一个不错的变种。
import torch
from torch.autograd import Variable
# number of neurons in each layer
input_num_units = 28*28
hidden_num_units = 500
output_num_units = 10
# set remaining variables
epochs = 5
batch_size = 128
learning_rate = 0.001
b)训练模型
# define model
model = torch.nn.Sequential(
torch.nn.Linear(input_num_units, hidden_num_units),
torch.nn.ReLU(),
torch.nn.Linear(hidden_num_units, output_num_units),
)
loss_fn = torch.nn.CrossEntropyLoss()
# define optimization algorithm
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
## helper functions
# preprocess a batch of dataset
def preproc(unclean_batch_x):
"""Convert values to range 0-1"""
temp_batch = unclean_batch_x / unclean_batch_x.max()
return temp_batch
# create a batch
def batch_creator(batch_size):
dataset_name = 'train'
dataset_length = train_x.shape[0]
batch_mask = rng.choice(dataset_length, batch_size)
batch_x = eval(dataset_name + '_x')[batch_mask]
batch_x = preproc(batch_x)
if dataset_name == 'train':
batch_y = eval(dataset_name).ix[batch_mask, 'label'].values
return batch_x, batch_y
# train network
total_batch = int(train.shape[0]/batch_size)
for epoch in range(epochs):
avg_cost = 0
for i in range(total_batch):
# create batch
batch_x, batch_y = batch_creator(batch_size)
# pass that batch for training
x, y = Variable(torch.from_numpy(batch_x)), Variable(torch.from_numpy(batch_y), requires_grad=False)
pred = model(x)
# get loss
loss = loss_fn(pred, y)
# perform backpropagation
loss.backward()
optimizer.step()
avg_cost += loss.data[0]/total_batch
print(epoch, avg_cost)
# get training accuracy
x, y = Variable(torch.from_numpy(preproc(train_x))), Variable(torch.from_numpy(train_y), requires_grad=False)
pred = model(x)
final_pred = np.argmax(pred.data.numpy(), axis=1)
accuracy_score(train_y, final_pred)
# get validation accuracy
x, y = Variable(torch.from_numpy(preproc(val_x))), Variable(torch.from_numpy(val_y), requires_grad=False)
pred = model(x)
final_pred = np.argmax(pred.data.numpy(), axis=1)
accuracy_score(val_y, final_pred)
训练分数是:
0.8779008746355685
验证分数是:
0.867482993197279
这个分数相当的高,我们才训练这个简单的神经网络五个周期而已。

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
上一篇
用于机器学习的线性代数速查表
下一篇
机器学习优化函数的直观介绍
热门企业
热门职位
写评论取消
回复取消






























