用于组合优化的强化学习:学习策略解决复杂的优化问题
2019年04月20日 由 明知不问 发表
834870
0
 从人类诞生之初,每一项技术创新,每一项改善我们生活的发明都是经过奇思妙想后设计出来的。从火到车轮,从电力到量子力学,我们对世界的理解和我们周围事物的复杂性,已经增长到难以直观地掌握它们的程度。
从人类诞生之初,每一项技术创新,每一项改善我们生活的发明都是经过奇思妙想后设计出来的。从火到车轮,从电力到量子力学,我们对世界的理解和我们周围事物的复杂性,已经增长到难以直观地掌握它们的程度。如今,飞机,汽车,船舶,卫星等复杂结构的设计者在很大程度上依赖于算法,使其变得更完美,这通常是人类无法以微妙的形式实现的。除了设计之外,优化在日常事务中起着至关重要的作用,例如网络路由(互联网和移动),物流,广告,社交网络甚至医学。
在未来,随着我们的技术不断改进和复杂化,对解决大规模难题的能力可能会有更高的要求,并且需要在优化算法方面取得突破。
组合优化问题
从广义上讲,组合优化问题涉及从有限的一组对象中找到“最佳”对象。在这种情况下,“最佳”是通过给定的评估函数来测量的,该函数将对象映射到某个分数或成本,目标是找到最低成本的对象。大多数实际中有趣的组合优化问题也非常困难,因为即使问题的大小只增加了一点,集合中的对象数量也会以极快的速度增加,导致穷举搜索不切实际。
为了讲这件事解释清楚,我们将专注于一个特定的问题,即着名的旅行商问题(TSP)。假设我们有N个城市,我们的销售员必须全部访问它们。然而,在城市之间穿梭会产生一些费用,我们必须找到一种方案,在旅行到所有城市并返回起始城市过程中最大限度地减少总累积成本。例如,下图显示了美国所有省会城市的最佳旅游路线:
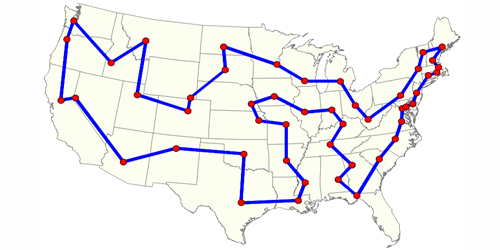
这个问题出现在许多重要的应用中,例如计划,交付服务,制造,DNA测序等。寻找更好的旅行团队有时会产生严重的财务影响,促使科学界和企业投入大量精力来解决这些问题。
在用K个城市建立TSP实例之旅的同时,我们在旅游建设过程的每个阶段都去除了一个城市,直到不再有城市为止。在第一阶段,我们有K个城市可以选择,在第二阶段我们有K-1个,然后是K-2个,以此类推。我们可以构建的可能的游览数量是我们在每个阶段的选项数量的乘积,因此这个问题的复杂性表示为O(K!)。
如果数字较小,这并不困难:假设我们有5个城市,可能的旅行次数是5!= 120。但是对于7个城市,它增加到5040,对于10个城市,已经达到3628800,对于100个城市来说,它高达9.332622e + 157,这比宇宙中的原子数多出许多个数量级。
在现实世界中出现的TSP的实际实例通常包含数千个城市,为了在合理的时间(几个小时)内得到解决,需要开发了几十年的高度复杂的搜索算法和启发式算法。遗憾的是,在现实世界的应用程序中出现的许多COP具有独特的细微差别和约束,使我们无法仅使用最先进的方案解决TSP等已知问题,并且还要求我们开发针对该问题的方法和启发式算法。这个过程可能是漫长而艰巨的,并且可能需要领域专家来检测特定问题的组合搜索空间中的某些结构。
由于近年来深度学习在许多领域取得了巨大成功,让机器学会如何自己解决问题听起来非常有潜力。将算法设计自动化,可为COP节省大量的金钱和时间,而且可能产生比人类设计的方法更好的解决方案。
学习图形表示
2016年,一篇名为“Learning Combinatorial Optimization Algorithms over Graphs”的论文对这个问题进行了早期尝试。作者训练了一种叫做structure2vec的图神经网络,构建几个硬COP的解决方案,并获得非常好的近似比率(生产成本与最优成本之间的比率)。
其基本思想是:问题的状态可以表示为图形,在图形上,神经网络构建解决方案。在解决方案构建过程的每次迭代中,网络观察当前图形,并选择要添加到解决方案的节点,之后根据该选择更新图形,并且重复该过程直到获得完整的解决方案。
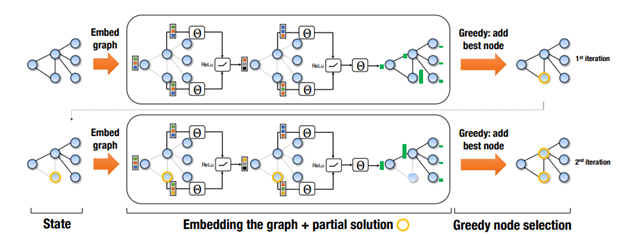
作者使用DQN算法训练神经网络,并证明了学习模型能够推广到比训练更大的问题实例。模型甚至可以顺利推广到1200个节点的实例(同时在大约100个节点的实例上进行训练),并且可以在12秒内生成解决方案,这些解决方案有时比在1小时内找到的商业解决方案更好。他们的方法的一大缺点是他们使用了辅助函数,以帮助神经网络找到更好的解决方案。这个辅助函数是人为设计的,并且是特定于问题的,而这正是我们想要避免的。
使用基于图形的状态表示非常有意义,因为许多COP可以通过这种方式非常自然地表达,如TSP图的示例中所示:
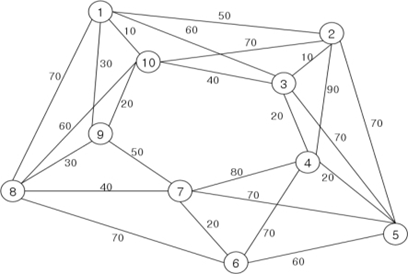
节点代表城市,边缘包含城市间距离。可以在没有边缘属性的情况下构建非常相似的图形(如果由于某种原因不假设距离的知识)。近年来,在图形上运行的神经网络模型(无论是否具有假设结构)越来越流行,最显著的是在自然语言处理领域,Transformer风格模型已成为许多任务的实现技术。
Transformer体系结构用于解决NLP中出现的序列问题。不同的是,在递归神经网络中,例如LSTMs,是显式地输入一个序列的输入向量,而Transformer是作为一组对象输入的,必须采取特殊的方法来帮助它看到序列中的顺序。Transformer使用由一个多头自注意子层和一个完全连接的子层组成的若干层。
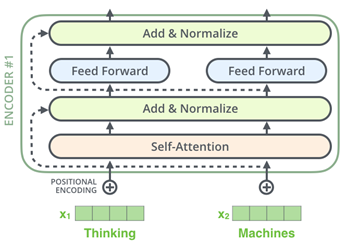
与图形的关系在注意层中变得明显,注意层实际上是输入“节点”之间的一种消息传递机制。每个节点都观察其他节点并参与那些看起来更有意义的节点。这与Graph Attention Networks发生的过程非常相似,事实上,如果我们使用掩码来阻止节点将消息传递给不相邻的节点,我们将获得一个等效的过程。
学会解决没有人类知识的问题
在论文“Attention! Learn to Solve Routing Problems”中(arxiv.org/pdf/1803.08475.pdf),作者解决了几个涉及在图形上路由代理的组合优化问题,包括我们现在讨论的旅行商问题。
将输入视为一个图形,并将其提供给一个经过修改的Transformer体系结构,该体系结构嵌入图的节点,然后依次选择要添加到tour的节点,直到构建完整的tour为止。
将输入作为图形处理比给它一系列节点更好,因为它消除了对输入中给出城市的顺序的依赖性,只要它们的坐标不变。这意味着,无论我们如何对城市进行排列,给定的图神经网络的输出都将保持不变,这与序列方法不同。
在本文提出的体系结构中,图形由transformer式编码器嵌入,为所有节点生成嵌入,并为整个图形生成单个嵌入向量。为了获取解决方案,单独的解码器网络每次赋予特殊上下文向量,即由图嵌入和那些最后和最前面的城市,和未访问城市的嵌入,并且它在未访问的输出概率分布,被抽样以生成下一个要访问的城市。解码器顺序产生城市直到游览完成,然后根据游览的长度给出奖励。
作者使用了一种增强学习算法来训练模型,这是一种基于策略梯度的算法。版本的伪代码如下:

他们使用roll-out network评估实例的难度,并使用策略网络的参数定期更新roll-out network。使用这种方法,作者在几个问题上取得了优异的成果,超越了前面几节中提到的其他方法。但是,他们仍然是在小型实例上训练和评估他们的方法,最多有100个节点。虽然这些结果很有希望,但与现实世界相比,依然微不足道。
扩展到大型问题
最近,通过“Learning Heuristics Over Large Graphs Via Deep Reinforcement Learning”一文(arxiv.org/pdf/1903.03332.pdf),研究者朝着现实世界的问题迈出了重要一步。在论文中,作者训练了一个图卷积网络来解决大型问题,如最小顶点覆盖(MVC)和最大覆盖问题(MCP)。他们使用流行的贪婪算法来训练神经网络嵌入图形,并预测每一阶段要选择的下一个节点,然后使用DQN算法对其进行进一步的训练。
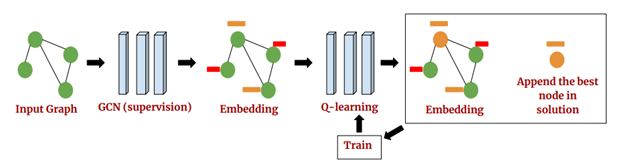
团队在具有数百万个节点的图表上评估了他们的方法,结果比当前标准算法更快更好。虽然他们确实利用手工制作的启发式方法来帮助训练模型,但未来的工作可能会消除这种限制,并学会解决类似Tabula Rasa的大型问题。
总的来说,在大量搜索空间问题中寻找结构的探索是强化学习的一个重要而实用的研究方向。强化学习的许多批评者声称,到目前为止,它只用于解决游戏和简单的控制问题,并且将其迁移到现实世界的问题仍然很遥远。
虽然这些说法也没错,但在本文中概述的方法代表了其非常真实的用途,可以在近期内为强化学习带来好处,而遗憾的是,它们不能像电子游戏方法那样吸引大量的关注。

欢迎关注ATYUN官方公众号
商务合作及内容投稿请联系邮箱:bd@atyun.com
上一篇
Python人脸检测指南(下)
下一篇
深度学习词汇表(四)
热门企业
热门职位
写评论取消
回复取消






























