最近，图神经网络（GNN）在各种领域越来越流行，包括社交网络，知识图，推荐系统，甚至生命科学。GNN在对图中节点之间的依赖关系建模方面的强大功能使得与图分析相关的研究领域取得了突破。本文旨在介绍图形神经网络的基础知识和两种更高级的算法，DeepWalk和GraphSage。

图

在我们学习GNN之前，让我们先了解一下图是什么。在计算机科学中，图是由两个组成部分组成的数据结构，即顶点和边缘。图G可以通过顶点集V和它包含的边E来进行描述。



边可以是有向的或无向的，这取决于顶点之间是否存在方向依赖关系。

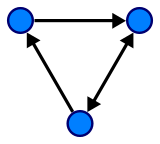
有向图

顶点通常称为节点。在本文中，这两个术语是可以互换的。

GNN

GNN是一种直接在图结构上运行的神经网络。GNN的典型应用是节点分类。本质上，图中的每个节点都与一个标签相关联，我们希望预测没有地面实况的节点的标签。本节将说明本文中描述的算法，GNN的第一个提议，因此通常被视为原始GNN。

在节点分类问题设置中，每个节点v的特征在于其特征x_v并且与地面实况标签t_v相关联。给定部分标记的图G，目标是利用这些标记的节点来预测未标记的节点的标签。它学习用包含邻域信息的d维向量（状态）h_v表示每个节点：



其中x_co[v]表示与v相连的边的特征，h_ne[v]表示v相邻节点的嵌入，x_ne[v]表示v相邻节点的特征。函数f是将这些输入投影到d维空间上的过渡函数。由于我们在寻找h_v的唯一解，我们可以应用Banach不动点定理，将上面的方程重写为迭代更新过程。



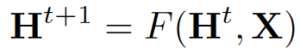
H和X分别表示所有h和x的串联。

GNN的输出是通过将状态h_v和特性x_v传递给输出函数g来计算的。



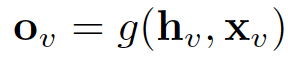
这里的f和g都可以解释为前馈全连通神经网络。L1损失可以直接表述为：



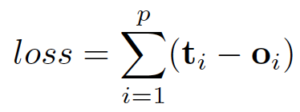
可以通过梯度下降优化。

但是，有论文指出了GNN的原始提议有三个主要的限制：

1. 如果放宽了“固定点”的假设，则可以利用多层感知器来学习更稳定的表示，并删除迭代更新过程。这是因为，在原始提议中，不同的迭代使用相同的转换函数f的参数，而MLP的不同层中的不同参数允许分层特征提取。


2. 它不能处理边缘信息（例如，知识图中的不同边缘可能表示节点之间的不同关系）


3. 固定点可以阻止节点分布的多样化，因此可能不适合学习表征节点。

已经有几种GNN变体来解决上述问题。但是它们不是这篇文章的重点。

DeepWalk

DeepWalk是第一个提出无监督学习节点嵌入的算法。它在训练过程中类似于单词嵌入。其动机是图中节点和语料库中单词的分布都遵循幂律，如下图所示：



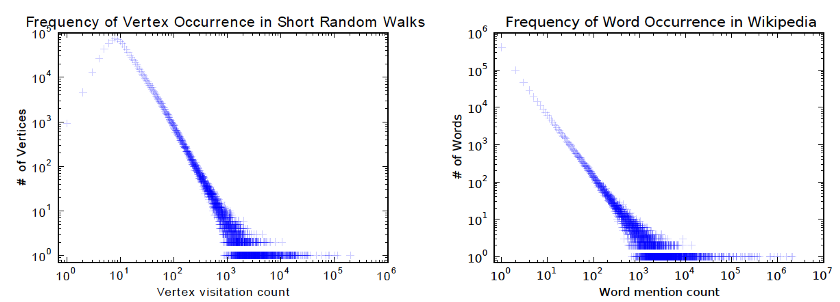
该算法包含两个步骤：

1. 在图中的节点上执行随机遍历以生成节点序列


2. 运行skip-gram，根据步骤1中生成的节点序列学习每个节点的嵌入

在随机游走的每个时间步骤，下一个节点从上一个节点的邻节点均匀采样。然后将每个序列截断为长度为2|w| + 1的子序列，其中w为跳变图中的窗口大小。

在本文中，分层softmax用于解决由于节点数量庞大而导致的softmax计算成本高昂的问题。为了计算每个单独输出元素的softmax值，我们必须计算所有元素k的所有e ^ xk。

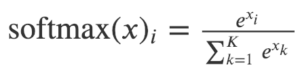
Softmax的定义

因此，原始softmax的计算时间为O（| V |），其中V表示图中的顶点集合。

分层softmax利用二叉树来处理问题。在这个二叉树中，所有叶子（上图中的v1，v2，... v8）都是图中的顶点。在每个内部节点中，有一个二元分类器来决定选择哪条路径。

为了计算给定顶点v_k的概率，可以简单地计算沿着从根节点到离开v_k的路径中的每个子路径的概率。由于每个节点的子概率为1，因此所有顶点的概率之和等于1的特性仍然保持在分层softmax中。由于二叉树的最长路径以O（log（n））为界，因此元素的计算时间现在减少为O（log | V |），其中n是叶子节点的数量。

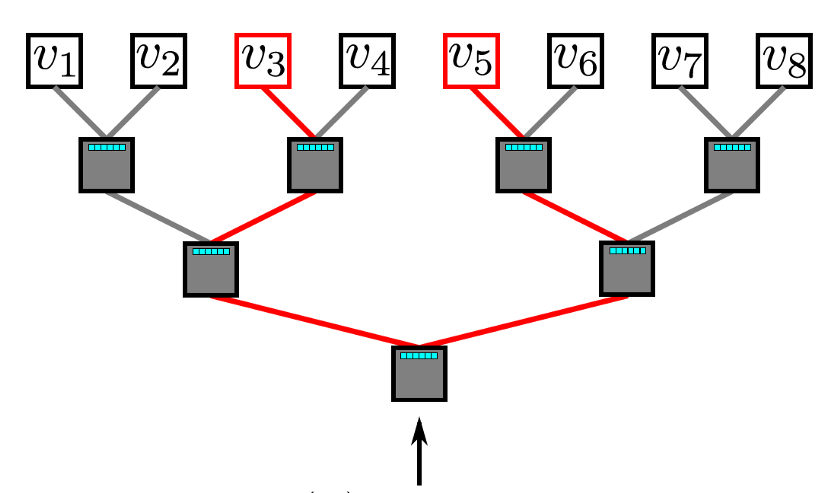
分层Softmax

在训练DeepWalk GNN之后，模型已经学习了每个节点的良好表示，如下图所示。不同的颜色表示输入图中的不同标签。我们可以看到，在输出图形（嵌入2维）中，具有相同标签的节点聚集在一起，而具有不同标签的大多数节点被正确地分开。



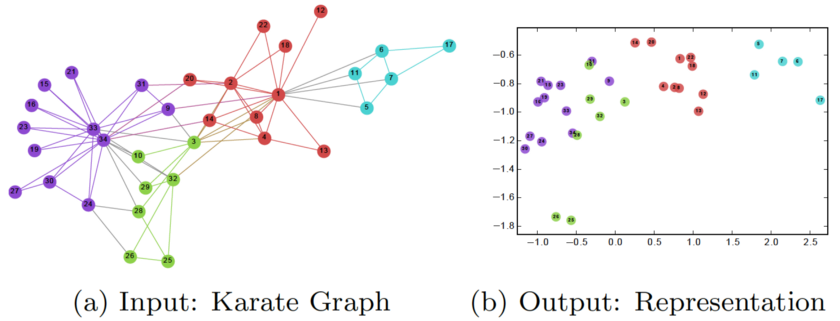
然而，DeepWalk的主要问题是它缺乏泛化能力。每当有新节点进入时，它必须重新训练模型以表示该节点（转换）。因此，这种GNN不适用于图中节点不断变化的动态图。

GraphSage

GraphSage提供解决上述问题的解决方案，以归纳方式学习每个节点的嵌入。具体而言，每个节点由其邻域的聚合表示。因此，即使在训练时间期间看不到的新节点出现在图中，它仍然可以由其相邻节点正确地表示。下面显示了GraphSage的算法。



外环表示更新迭代次数，而h ^ k_v表示更新迭代k时节点v的潜在向量。在每次更新迭代时，基于聚合函数，前一次迭代中v和v的邻域的潜在向量以及权重矩阵W ^ k来更新h ^ k_v。本文提出了三种聚合函数：

1.平均聚合器：

平均聚合器获取节点及其所有邻域的潜在向量的平均值。



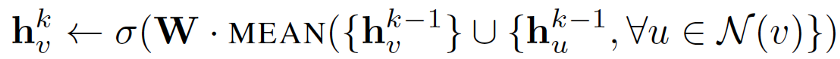
与原始方程相比，它删除了上述伪代码中第5行的连接操作。此操作可以被视为“跳过连接”，本文稍后将证明它可以在很大程度上提高模型的性能。

2. LSTM聚合器：

由于图中的节点没有任何顺序，因此它们通过置换这些节点来随机分配顺序。

3.池化聚合器：

此运算符在相邻集上执行逐元素池化功能。下面显示了最大化池化的示例：



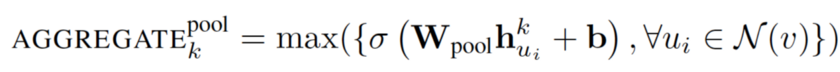
它可以用平均池化或任何其他对称池化函数替换。它指出池化聚合器执行最佳，而均值池化和最大化池化聚合器具有相似的性能。本文使用最大化池化作为默认池化函数。

损失函数定义如下：



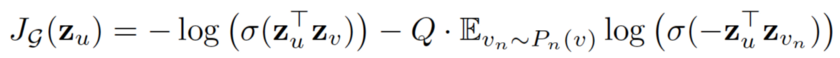
其中u和v共同出现在固定长度的随机游走中，而v_n是不与u共同出现的负样本。这种损失函数鼓励节点更接近具有类似的嵌入，而距离较远的节点则在投影空间中被分离。通过这种方法，节点将获得越来越多关于其邻域的信息。

GraphSage通过聚合其附近的节点，可以为看不见的节点生成可表征的嵌入。它允许将节点嵌入应用于涉及动态图的域，其中图的结构不断变化。例如，Pinterest采用了GraphSage的扩展版本PinSage，作为其内容发现系统的核心。

结论

这就是有关GNN，DeepWalk和GraphSage的基础知识。GNN在复杂图形结构建模中的强大功能确实令人惊讶。鉴于其有效性，在不久的将来，GNN将在AI的发展中发挥更为重要作用。