最小二乘法从何而来
在机器学习面试中,如果被问及最小二乘损失函数的数学基础,你会怎么回答?
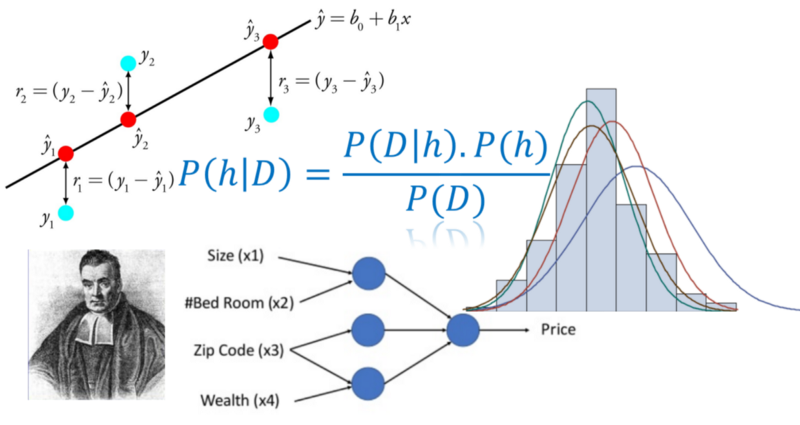
问:为什么在回归机器学习任务中对误差进行平方?
答:“为什么,当然是因为它将所有误差(残差)变成正数!”
问题:“好的,为什么不使用更简单的绝对值函数| x | 使所有的误差变为正数呢?“
答:“啊哈,你在误导我。绝对值函数不是处处可微的!“
问:“这对数值算法来说无关紧要。LASSO回归使用具有绝对值的项,它可以被处理。另外,为什么不用X的四次方或log(1 + X ²)?对误差进行平方有什么特别之处?
答:额......
贝叶斯论证
请记住,对于机器学习中的所有棘手问题,如果你在论证中混合使用“ 贝叶斯 ” 这个词,你就能回答出一个听起来很严肃的答案……好吧,这是逗你玩的。
但是,我们确实应该准备好讨论最流行的损失函数的来历,比如最小二乘法和交叉熵- 至少,当我们试图找到使用贝叶斯参数的监督学习问题的最可能假设时,我们需要这样这种了解。
基础知识:贝叶斯定理和“最可能的假设”
贝叶斯定理可能是现代机器学习和人工智能系统中最具影响力的概率论恒等式。这里不做直观的介绍,专注于方程。
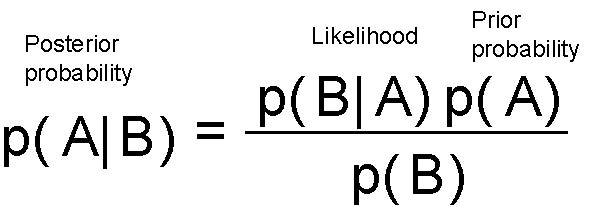
这本质上告诉你在看到数据/证据(可能性)后更新你的可信度(先验概率)并将更新的可信度分配给后验概率。你可以从一个可信度开始,但每个数据点都会强化或削弱这种可信度,并且你会一直更新你的假设。
现在让我们用不同的符号( 与数据科学有关的符号)重写贝叶斯定理 。让我们用d表示数据,用h表示假设。这意味着,给定数据后,我们可以应用贝叶斯的公式来尝试确定数据来自哪个假设。我们把定理重写为:
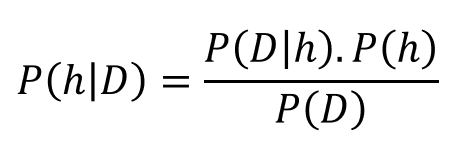
现在,一般来说,我们有一个很大的(通常是无限的)假设空间,也就是说,有许多假设可供选择。贝叶斯推断(或贝叶斯推理)的本质是我们想要检查数据以最大化一个最有可能产生观察数据的假设的概率。从根本上上说,我们想要确定P(h | D)的argmax,即我们想知道在给定观察到的D的情况下哪个h是最可能的。
最大似然
上面的等式看起来很简单,但在实际计算中却是出了名的难。因为在复杂的概率分布函数上评估积分时,假设空间非常大,而且计算起来很复杂。
然而,在寻找“给定数据中最可能的假设”的过程中,我们可以进一步简化它。
- 我们可以在分母中删除这个项,它没有包含h的项(即假设)。我们可以把它想象成一个使总概率总和为1的归一化器。
- 统一先验假设 - 通过使P(h)的性质一致,即所有假设都是可能的,这本质上放松了对P(h)性质的任何假设。然后是常数1 / | Vsd | 其中| Vsd | 是版本空间的大小,即与训练数据一致的所有假设的集合。然后,它实际上并未包括最大可能假设的确定。
在这两个简化假设之后,最大似然(ML)假设可以由下式给出,
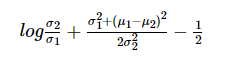
这仅仅意味着最可能的假设是观察数据的条件概率(给定假设)达到最大值的假设。
数据中的噪声
我们通常在Stats 101(统计课程)中学习简单线性回归时开始使用最小二乘误差(least-square error),但这种简单的损失函数几乎牢牢地驻留在每个监督机器学习算法中。如线性模型,样条函数,决策树或深度学习网络。
那么,有什么特别之处呢?它与贝叶斯推断有什么关系吗?
事实证明,最小二乘误差和贝叶斯推断之间的关键联系是假定误差或残差的性质。
观测数据一般都有误差,并且始终存在与数据相关的随机噪声。机器学习算法的任务是通过将信号与噪声分离来估计或近似可能生成数据的函数。
但是我们能说出这种噪音的本质吗?事实证明,噪声可以建模为随机变量。因此,我们可以将我们选择的概率分布与此随机变量相关联。
最小二乘优化的一个关键假设是残差的概率分布,即我们的老朋友 - 高斯正态分布。
这意味着监督学习训练数据集中的每个数据点(d)可以写为未知函数f(x)(学习算法试图近似的函数)与一个来自正态分布的零均值(μ)和未知方差σ²误差项的和,如下:
从这里,我们可以很容易地得出最大可能假设是最小化最小二乘方误差的假设。
警告:从ML假设中正式推导最小二乘优化准则无法绕过某些数学计算。
从最大似然假设推导出最小二乘

 最后圈住的部分是简单的最小二乘最小化(可以跳过这一节,我会在下一节中总结关键结论。)。
最后圈住的部分是简单的最小二乘最小化(可以跳过这一节,我会在下一节中总结关键结论。)。那么,所有这些数学表明了什么?
它表明,从监督训练数据集的误差分布在高斯分布的假设开始,该训练数据的最大可能假设是最小化最小平方误差损失函数的假设。
关于学习算法的类型没有假设。这同样适用于从简单线性回归到深度神经网络。
以下是线性回归拟合的经典场景。贝叶斯推断论证适用于该模型,并且使误差平方成为最佳损失函数的选择具有可信度。
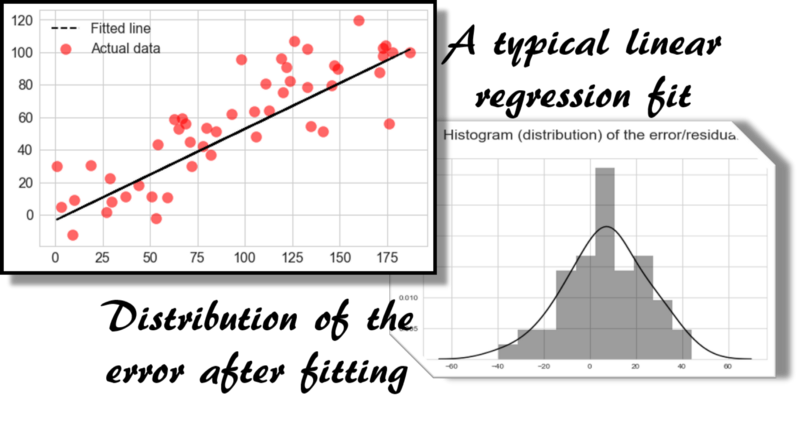
常态的假设是否足够?
你可以质疑关于正态分布误差项假设的有效性。但在大多数情况下,它都有效。这是从中心极限定理(CLT)得出的,因为误差或噪声永远不会由单个基础过程产生,而是从多个子过程的综合影响中产生。当大量随机子过程结合时,它们的平均值遵循正态分布。因此,对于我们大多数机器学习任务来说,假设这样的分布假设这样的分布并不过分。
另一个(更有力的)论据是高斯—马尔可夫定理
事实证明,在没有关于误差分布的信息的情况下,最小二乘法仍然是所有线性估计中最好的线性无偏估计(根据高斯—马尔可夫定理)。唯一的要求是误差的期望值为零,不相关且具有相等的方差。
类似的论证是否适用于分类问题?
最小二乘损失函数用于回归任务。但是如果我们处理类和概率的分类问题而不是任意实数呢?事实证明,类似的推导可以使用ML假设和简单的类定义选择来实现:
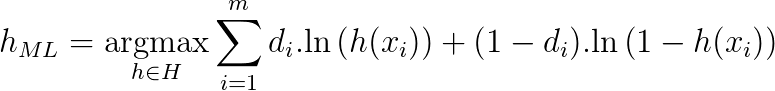
这只是交叉熵损失函数。
因此,相同的贝叶斯推断得到的交叉熵作为损失函数的首选,以获得分类问题中的最大可能假设。
结论
我们可以通过以下几点总结和扩展我们在文章中的讨论和论点,
- 最大似然估计(MLE)是一种强大的技术,如果我们可以做出统一的先验假设(即在开始时,所有假设都是同等可能的),那么就可以得出给定数据集的最可能假设。
- 如果我们可以假设机器学习任务中的每个数据点都是真实的函数和一些正态分布的随机噪声变量之和,那么我们可以推导出最大可能假设是最小化平方损失函数的假设。
- 这个结论与机器学习算法的本质无关。
- 另一个隐含的假设是数据点的相互独立,这使我们能够将联合概率写为个体概率的简单乘积。这也强调了在建立机器学习模型之前消除训练样本之间共线性的重要性。































