赫尔辛基大学AI基础教程:朴素贝叶斯分类(3.3节)
赫尔辛基大学AI基础教程合集:赫尔辛基大学AI基础教程
本章中,我们将学习朴素贝叶斯分类。
贝叶斯定理最有用的应用之一就是所谓的朴素贝叶斯分类。贝叶斯分类是一种可用于分类的机器学习技术,比如将文本文档等对象分为两类或更多类。通过分析一组训练数据来训练分类器,以此给出正确的类别。
朴素贝叶斯分类可用于确定给定大量不同观察值的类的概率。模型中假设,在给定类的情况下,特征变量是有条件独立的。(我们不会在这里讨论条件独立的含义,就我们的目的而言,在构建分类器时能够利用条件独立就足够了。)
实际应用:垃圾邮件过滤
我们以垃圾邮件过滤器作为演示朴素贝叶斯分类思想的运行示例。因此,类变量指示消息是垃圾邮件还是它是合法邮件。消息中的单词对应于特征变量,因此模型中的特征变量的数量由消息的长度决定。
注意
为什么要叫它“朴素”贝叶斯
以垃圾邮件过滤器为例,其想法是将语句视为通过选择一个接一个单词而产生,以便单词的选择仅取决于邮件是否是垃圾邮件。这是对过程的粗略简化,因为它意味着相邻单词之间不存在依赖关系,并且单词的顺序没有意义。所以这个方法被称为“朴素”。
上述想法通常使用以下图示来描述,其中消息类别(垃圾邮件或合法邮件)是影响单词的唯一因素。


尽管看起来简陋,朴素的贝叶斯方法在实践中往往工作得很好。这是证明统计学常用语,“所有模型都是错误的,但有些是有用的”的一个很好的例子。(这句格言通常被认为是统计学家George EP Box说的)
估计参数
首先,我们需要指定垃圾邮件的先前赔率(相对于合法邮件)。为了简单起见,假设为1:1,这意味着平均一半的收入消息是垃圾邮件。(现实中,垃圾邮件比例可能更大)
为了得到我们的似然比,我们需要两种不同的概率来表示任何单词的发生:一个在垃圾邮件中,另一个在合法邮件中。
这两个类的单词发行版最好是根据包含一些垃圾邮件消息和合法邮件消息的实际训练数据进行估计。最简单的方法是计算每个单词,如abacus,acacia,...,zurg出现在数据中的次数,并将数字除以总词数。
为了说明这个想法,让我们假设我们有一些垃圾邮件和一些合法邮件。您可以通过将一批电子邮件保存在两个文件中来轻松获取这些数据。
假设我们计算了两类消息中下列单词(连同所有其他单词)的出现次数:
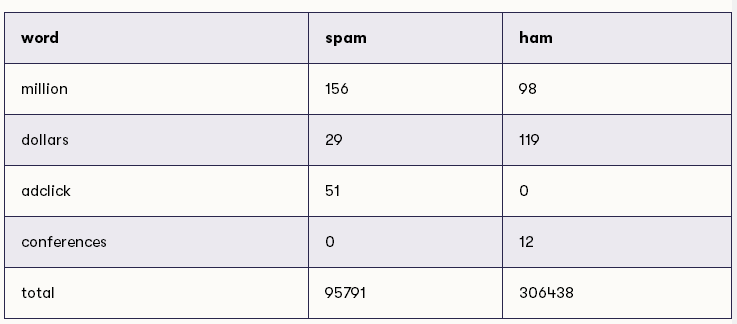
例如,我们现在可以估计,垃圾邮件中的单词为million的概率在95791中大约为156,大约等于614个单词中的1个。同样,我们可以估计在一条合法消息中单词million的概率,306438个单词中有98个单词,大约相当于3127个单词中的1个。这两种概率估计都很小,小于500分之一,但重要的是,前者高于后者:1 / 614高于1 / 3127。这意味着似然比,即第一个比例除以第二个比例大于1。更确切地说,该比率是(1/614)/(1/3127)= 3127/614 = 5.1(保留一位小数)。
注意
零意味着麻烦
直接从计数中估计概率的一个问题是零计数导致零估计。这对分类器的性能是非常有害的—它很容易导致后验概率为0/0的情况,这是无稽之谈。最简单的解决方案是对所有概率估计使用一个极小的下界。例如,值1:100000,这样就可以解决这个问题。
使用上述的逻辑,我们可以确定所有可能词的似然比,似然比如下:
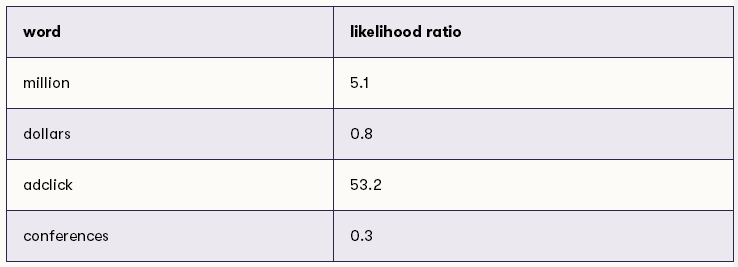
现在我们准备应用该方法对新消息进行分类。
例如:是垃圾邮件还是合法邮件?
一旦我们有了先验概率和估计的似然比,我们就可以应用贝叶斯规则了,这是我们在医学诊断案例中已经实践过的例子。推理过程与之前一样:我们通过将垃圾邮件的概率乘以似然比来更新垃圾邮件的赔率。为了深入记忆,我们先尝试一条单条消息的消息。对于先验赔率,如上所述,你应该使用赔率1:1。
练习12:一个单词的垃圾邮件过滤器
让我们从一个只有一个词的消息开始:“million”。
你的任务:使用上面的表格计算给出这个词的垃圾邮件的后验赔率。请记住,赔率与概率不一样,概率我们通常会表示为一个百分比。
以x.x的形式给出答案。
为了处理消息中的其他单词,我们可以使用完全相同的步骤。在上一个练习中计算出的一个单词之后的后验概率将成为下一个单词的先验概率,依此类推。
练习13:完整的垃圾邮件过滤器
现在使用朴素贝叶斯方法计算垃圾邮件的后验概率,给出信息为“million dollars adclick conferences”。
你应该再次从先验赔率1:1开始,然后将这些赔率重复乘以四个单词中每一个的似然比。上面列出了似然比可以供你参考。
您的任务:将结果表示为后验赔率,不对结果进行四舍五入。
练习10:贝叶斯定理(第1部分)
应用贝叶斯法则来计算在赫尔辛基早晨观测到的云之后降雨的后验概率。
正如我们上面计算的那样,观测到的云降雨的先验概率是206:159,似然比是 9。
以赔率形式给出结果,xx:yy,其中xx和yy是数字。请记住,当乘以赔率时,你应该只乘以分子部分(xx部分)。给出没有简化的答案(即使两边有同一公分母)。
答案:1854:159
练习11:贝叶斯定理(第2部分)
思考上述乳腺癌的情况。一名普通妇女进行X光照相检查,得到阳性检测结果,提示乳腺癌。你认为她患有乳腺癌的几率是多少?
使用你的直觉而不应用贝叶斯定理,并记录下来,你认为在阳性检查结果之后,她实际患乳腺癌的几率是多少。然后,使用贝叶斯定理计算患乳腺癌的后验概率。
首先计算先验赔率,然后乘以似然比。
以xx:yy形式给出答案,其中xx和yy是数字,给出没有简化的答案(即使两边有同一公分母)。
答案:40:95































